Линейны пространства сигналов
Линейное пространство – это множество элементов, которые называют векторами, и для которых справедливо:
1) Для каждой пары векторов 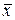 и
и 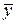 из множества существует вектор
из множества существует вектор 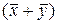 , принадлежащий этому же множеству и называемый их суммой
, принадлежащий этому же множеству и называемый их суммой 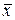 и
и 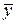 , такой, что выполняются свойства:
, такой, что выполняются свойства:
а) 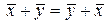 - коммутативность;
- коммутативность;
б) 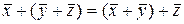 - ассоциативность; (1.2.5а)
- ассоциативность; (1.2.5а)
в) 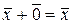 , где
, где 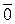 - нулевой элемент, единственный в множестве;
- нулевой элемент, единственный в множестве;
г) 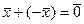 , причем
, причем 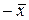 - единственный в множестве векторов.
- единственный в множестве векторов.
2) Имеется множество элементов, которые называются скалярами и образуют поле. При этом операция умножения вектора на скаляр ставит любому скаляру 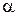 и любому вектору
и любому вектору 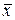 в соответствие вектор
в соответствие вектор 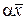 . При этом выполняются свойства:
. При этом выполняются свойства:
а) 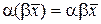 - ассоциативность;
- ассоциативность;
 - дистрибутивность;
- дистрибутивность;
г) 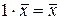 ,
, 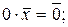 .
.
Заметим, что линейное пространство содержит два различных нуля при сложении: один для векторов ( 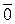 - нулевой элемент), другой для скаляров.
- нулевой элемент), другой для скаляров.
В теории сигналов обычно рассматриваются линейные пространства сигналов с конечными полями скаляров (например, бинарные, в которых используются только 0 и 1. Поэтому отождествлять поле скаляров с множеством всех действительных чисел не всегда удобно.
Если в качестве скаляров взяты действительные числа, линейное пространство называется действительным линейным пространством, если комплексные, то - комплексным линейным пространством.
Вектор
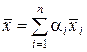 , (1.2.6)
, (1.2.6)
образованный суммированием нескольких векторов со скалярными коэффициентами, называется линейной комбинацией. Множество всех линейных комбинаций векторов 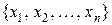 образует линейное пространство. Множество сигналов называется линейно независимым, если равенство
образует линейное пространство. Множество сигналов называется линейно независимым, если равенство
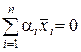 (1.2.7)
(1.2.7)
справедливо только при всех 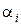 , равных нулю. Таким образом, в линейно независимом пространстве вектор не может быть представлен в виде линейной комбинации других векторов.
, равных нулю. Таким образом, в линейно независимом пространстве вектор не может быть представлен в виде линейной комбинации других векторов.
Пусть 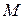 – пространство линейных комбинаций
– пространство линейных комбинаций 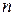 линейно независимых векторов
линейно независимых векторов 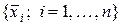 . Тогда каждый вектор в
. Тогда каждый вектор в 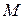 соответствует единственной линейной комбинации векторов
соответствует единственной линейной комбинации векторов 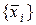 , т.е. единственному множеству скалярных коэффициентов. При этом
, т.е. единственному множеству скалярных коэффициентов. При этом 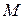 является
является 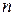 ‑мерным линейным пространством. Множество
‑мерным линейным пространством. Множество 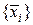 называют базисом для
называют базисом для 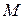 и говорят, что
и говорят, что 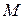 натянуто на этом базисе. Заметим, что линейное пространство имеет множество базисов, т.к. базисом может служить любое множество линейно независимых векторов.
натянуто на этом базисе. Заметим, что линейное пространство имеет множество базисов, т.к. базисом может служить любое множество линейно независимых векторов.
Например, пусть  ,
, 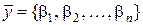 - упорядоченные последовательности из
- упорядоченные последовательности из 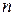 чисел. Тогда при сложении имеем:
чисел. Тогда при сложении имеем:
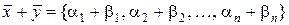 , (1.2.8)
, (1.2.8)
а при умножении:
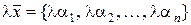 . (1.2.9)
. (1.2.9)
Очевидно, что любой вектор в 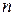 ‑мерном пространстве можно представить в виде линейной комбинации
‑мерном пространстве можно представить в виде линейной комбинации
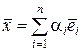 , (1.2.10)
, (1.2.10)
где
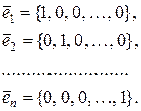 (1.2.11)
(1.2.11)
Заметим, что упорядоченную последовательность скалярных коэффициентов 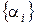 или
или 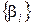 также можно трактовать как вектор. Тогда можно говорить, что имеется однозначное соответствие между векторами в пространстве
также можно трактовать как вектор. Тогда можно говорить, что имеется однозначное соответствие между векторами в пространстве 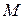 и векторами в пространстве
и векторами в пространстве 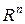 или
или 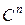 .
.
Дата добавления: 2016-11-04; просмотров: 1727;











