Пространства сигналов со скалярным произведением
Для улучшения структуры пространства сигналов вводят еще одну геометрическую характеристику – скалярное произведение двух сигналов (векторов), являющуюся отображением упорядоченных пар сигналов линейного пространства в комплексную плоскость  (в частном случае на действительную ось). Скалярное произведение будем обозначать как
(в частном случае на действительную ось). Скалярное произведение будем обозначать как 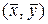 . При этом оно должно удовлетворять следующим условиям:
. При этом оно должно удовлетворять следующим условиям:
1) 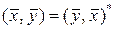 ;
;
2)  ; (1.2.16)
; (1.2.16)
3) 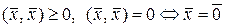 .
.
Покажем, что
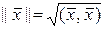 (1.2.17)
(1.2.17)
есть норма линейного пространства и удовлетворяет требованиям (1.2.12). Очевидно, что условия
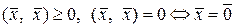 и
и 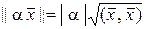
выполняются по определению. Покажем, что выполняется и неравенство треугольника. Для этого предварительно докажем, что
 . (1.2.18)
. (1.2.18)
Возьмем вектор 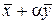 , где
, где 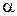 - скаляр. По определению
- скаляр. По определению
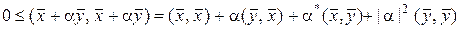 . (1.2.19)
. (1.2.19)
Положив 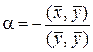 , из (2.19) получаем неравенство
, из (2.19) получаем неравенство
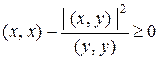 , (1.2.20)
, (1.2.20)
из которого сразу следует (1.2.18).
Теперь докажем неравенство треугольника. Для этого используем равенство 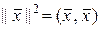 .
.
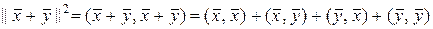 ,
,
где
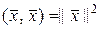 ,
, 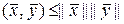 ,
, 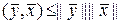 ,
, 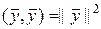 .
.
Тогда
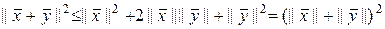 ,
,
откуда получаем
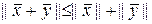 . (1.2.21)
. (1.2.21)
Таким образом, скалярное произведение сигналов порождает норму, а та в свою очередь - метрику.
Если пространство со скалярным произведением является метрически полным, то оно называется гильбертовым пространством сигналов.
Скалярное произведение часто интерпретируют как меру угла между векторами. Так, исходя из неравенства Шварца можно записать
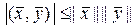 , (1.2.22)
, (1.2.22)
и тогда
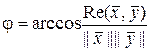 . (1.2.23)
. (1.2.23)
Очень часто используется понятие ортогональности векторов. Два вектора (сигнала) 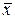 и
и 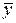 ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда 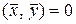 .
.
Приведем пример использования скалярного произведения для сигналов с ограниченной энергией. Пусть сигнал сдвигается во времени. Обозначим через 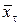 сигнал
сигнал 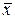 , сдвинутый во времени на
, сдвинутый во времени на 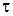 , т.е.
, т.е.
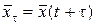 .
.
Тогда для пространства 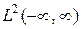 имеем
имеем
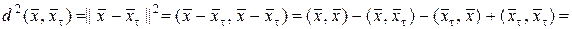
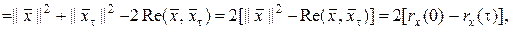 (1.2.24)
(1.2.24)
где 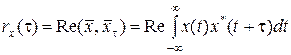 .
.
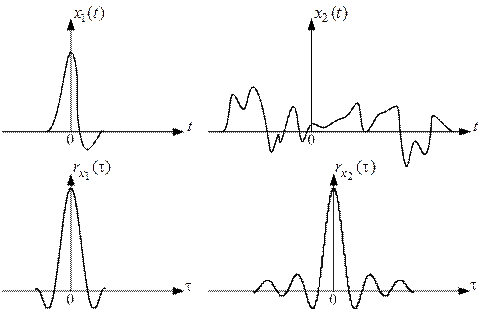
Таким образом, каждому сигналу 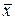 ставится в соответствие действительная функция от временного сдвига, которая определяет вызванное таким сдвигом смещение точки, изображающей сигнал в пространстве сигналов. Для быстро изменяющихся сигналов
ставится в соответствие действительная функция от временного сдвига, которая определяет вызванное таким сдвигом смещение точки, изображающей сигнал в пространстве сигналов. Для быстро изменяющихся сигналов 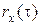 уменьшается (сужается) с ростом
уменьшается (сужается) с ростом 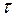 . В случае короткого сигнала
. В случае короткого сигнала 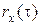 , будет узкой, но, как видно из рис. 1.6, и сигналу большой длительности может соответствовать «узкая»
, будет узкой, но, как видно из рис. 1.6, и сигналу большой длительности может соответствовать «узкая» 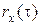 . При решении многих практических задач используют сигналы с узкой
. При решении многих практических задач используют сигналы с узкой 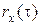 . Например, в радиолокации, где эту функию называют сечением функции неопределенности вдоль оси времени
. Например, в радиолокации, где эту функию называют сечением функции неопределенности вдоль оси времени 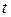 , это позволяет с высокой точностью измерить время прихода сигнала. При исследовании случайных сигналов ту же функцию называют автокорреляционной функцией сигнала
, это позволяет с высокой точностью измерить время прихода сигнала. При исследовании случайных сигналов ту же функцию называют автокорреляционной функцией сигнала 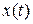 .
.
1.2.6. Представление элементов векторного пространства со
скалярным произведением
Существует прямая связь между сигналом и его представлением. Предположим, что 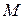 - произвольное
- произвольное 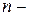 мерное пространство, натянутое на базис
мерное пространство, натянутое на базис 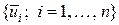 , тогда для
, тогда для 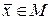 имеем
имеем
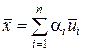 . (1.2.26)
. (1.2.26)
Если левую и правую часть умножить скалярно на 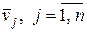 , то
, то
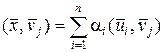 . (1.2.27)
. (1.2.27)
Получим систему линейных скалярных уравнений, решив которую относительно вектор-строки 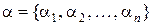 получим представление
получим представление 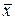 в пространстве
в пространстве 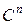 относительно базиса
относительно базиса 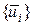 .
.
Выберем 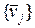 так, чтобы они были попарно ортогональны к
так, чтобы они были попарно ортогональны к 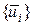 , т.е.
, т.е.
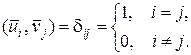 (1.2.28)
(1.2.28)
Тогда получаем
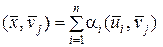
Откуда
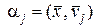 . (1.2.29)
. (1.2.29)
Базис 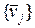 , удовлетворяющий (1.2.28), называется взаимным базисом, для которого при любом
, удовлетворяющий (1.2.28), называется взаимным базисом, для которого при любом 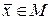 получаем
получаем
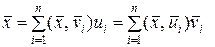 . (1.2.30)
. (1.2.30)
Очень удобно использование в качестве базиса в 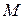 ортонормальной системы. Напомним, что система векторов называется ортонормальной, если взаимным базисом для нее является она сама. При этом все векторы взаимно ортогональны и их норма равна единице:
ортонормальной системы. Напомним, что система векторов называется ортонормальной, если взаимным базисом для нее является она сама. При этом все векторы взаимно ортогональны и их норма равна единице:
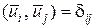 . (1.2.31)
. (1.2.31)
Тогда для любого сигнала 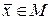 имеем
имеем
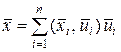 . (1.2.32)
. (1.2.32)
То есть получаем взаимно-однозначное соответствие между векторами в 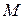 и их представлением в
и их представлением в 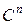 . В этом случае обеспечивается равенство скалярных произведений в векторном и скалярном пространствах (). Так для
. В этом случае обеспечивается равенство скалярных произведений в векторном и скалярном пространствах (). Так для  и
и 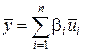 имеем
имеем
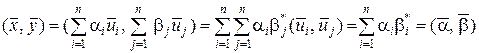 . (1.2.33)
. (1.2.33)
Важное значение имеет построение ортогональных базисов. Одним из наиболее употребляемых способов при этом является так называемый рекуррентный способ ортогонализации Грама-Шмидта, который заключается в следующем.
Пусть в 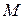 задана система
задана система 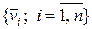 линейно независимых векторов. Тогда система ортонормальных векторов
линейно независимых векторов. Тогда система ортонормальных векторов 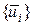 получается путем нормализации вспомогательных векторов
получается путем нормализации вспомогательных векторов  по следующему правилу:
по следующему правилу:
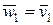 ,
, 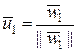 ,
,
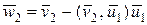 ,
, 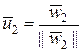 ,
,
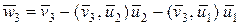 ,
, 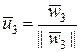 , (1.2.34)
, (1.2.34)
. . . . . . .
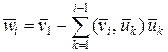 ,
, 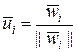 .
.
Заметим, что если функции 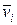 переставить местами, то получим другую, но тоже ортонормальную систему.
переставить местами, то получим другую, но тоже ортонормальную систему.
Рассмотрим пример. Применим процедуру Грама-Шмидта к последовательности функций 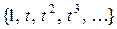 , определенных на отрезке
, определенных на отрезке 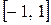 . В этом случае
. В этом случае 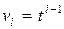 .
.
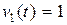 ,
, 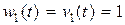 ,
,  ,
,
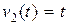 ,
, 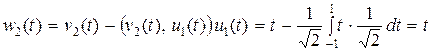 ,
, 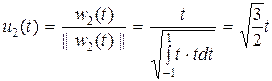 ,
,
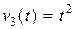 ,
,
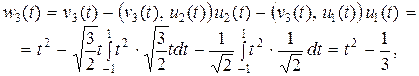
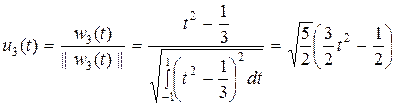 ,
,
. . . . . . .
Дата добавления: 2016-11-04; просмотров: 2202;











