Нормированные линейные пространства сигналов

Для улучшения геометрических свойств линейного пространства сигналов определяют действительное число, характеризующее «размер» сигнала 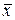этого пространства, которое называется нормой вектора и обозначается . Норма должна удовлетворять следующим требованиям:

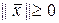1. и ;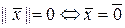

2. 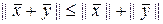; (1.2.12)

3. .

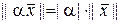Тогда

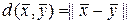(1.2.13)

метрика, которая делающая линейное пространство сигналов метрическим. Норма сигнала равна расстоянию точки от начала координат до точки в пространстве сигналов, соответствующая этому сигналу.

Норма сигнала объединяет геометрические свойства метрического пространства и алгебраические свойства линейного прогстранства.

Нормированное линейное пространство сигналов, являющееся полным метрическим, называется банаховым пространством.

Для упорядоченных последовательностей действительных или комплексных чисел норму обычно определяют соотношением:

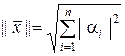, (1.2.14)

а для действительных или комплексных функций времени, характеризующих сигналы, заданные на интервале времени 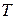- соотношением

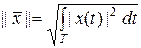. (1.2.15)

Последнее соотношение имеет простую физическую интерпретацию: квадрат нормы является энергией сигнала. Началом координат здесь является функция, равная нулю почти всюду на всем интервале 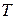. Заметим, что множество функций, для которых норма (1.2.15) ограничена, называется пространством 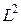и часто обозначается .

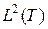При этом справедливы общепринятые обозначения для временных интервалов

;

; ,

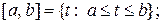
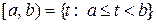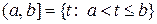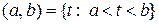пространства 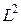, например, 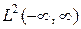, , 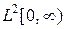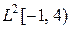и т.д.