Дискретное представление сигналов
1.3.1. Подпространства сигналов с конечной энергией ( 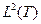 )
)
Рассмотрим задачу численного представления произвольного сигнала с ограниченной энергией 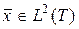 . Пусть нужно найти отображение
. Пусть нужно найти отображение 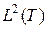 в пространство
в пространство 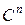 . При этом
. При этом 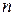 выбирается исходя из требуемой точности и экономичности представления сигналов. Так как число измерений пространства
выбирается исходя из требуемой точности и экономичности представления сигналов. Так как число измерений пространства 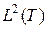 бесконечно (поскольку сигнал считаем произвольным), а
бесконечно (поскольку сигнал считаем произвольным), а 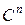 конечно, отображение должно быть типа «много в одно». При этом произвольный сигнал из
конечно, отображение должно быть типа «много в одно». При этом произвольный сигнал из 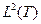 не может быть представлен в
не может быть представлен в 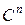 отлично от всех остальных сигналов. Поэтому пространство
отлично от всех остальных сигналов. Поэтому пространство 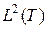 разбивается на множества эквивалентности, каждому из которых взаимно однозначно соответствует некоторая точка в
разбивается на множества эквивалентности, каждому из которых взаимно однозначно соответствует некоторая точка в 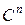 .
.
Выберем 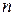 -мерное пространство следующим образом. Пусть
-мерное пространство следующим образом. Пусть 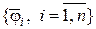 - система линейно-независимых функций из
- система линейно-независимых функций из 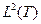 , таких, что при
, таких, что при 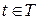 условие
условие
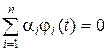 (1.3.1)
(1.3.1)
выполняется в том и только том случае, если 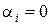 для всех
для всех 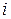 . Натянем на
. Натянем на 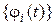 линейное подпространство
линейное подпространство 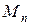 . Тогда сигнал
. Тогда сигнал 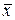 , принадлежащий
, принадлежащий 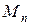 , может быть представлен
, может быть представлен 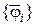 единственным образом в виде линейной комбинации:
единственным образом в виде линейной комбинации:
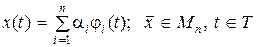 , (1.3.2)
, (1.3.2)
где коэффициенты 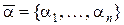 образует искомое представление в
образует искомое представление в 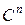 .
.
Поскольку 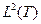 есть пространство со скалярным произведением и учитывая, что в соответствии с ()
есть пространство со скалярным произведением и учитывая, что в соответствии с ()
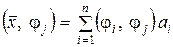 ,
, 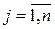 ,
,
отношением между 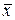 и
и 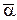 может быть выражено в матричной форме:
может быть выражено в матричной форме:
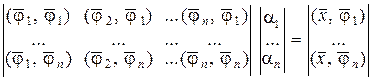
или
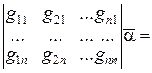
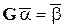 , (1.3.3)
, (1.3.3)
где: 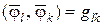 ;
; 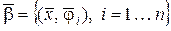 .
.
Откуда можно найти 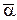 :
:
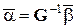 . (1.3.4)
. (1.3.4)
Для другого способа нахождения 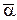 введём в
введём в 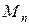 взаимные базисные функции
взаимные базисные функции 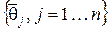 и выразим их через базисные функции
и выразим их через базисные функции 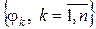 ,
,
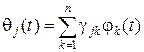 . (1.3.5)
. (1.3.5)
Опричем
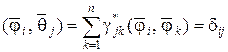 (1.3.6)
(1.3.6)
есть символ Кронекера.
Следовательно, в целом для системы:
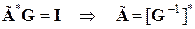 , (1.3.7)
, (1.3.7)
тогда
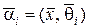 . (1.3.8)
. (1.3.8)
Заметим, что в обоих подходах нахождения коэффициентов разложения 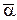 нужно вычислять обратные матрицы.
нужно вычислять обратные матрицы.
Теперь рассмотрим, как находить представление произвольного сигнала из 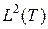 , не принадлежащего
, не принадлежащего 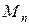 . Для этого произвольному вектору
. Для этого произвольному вектору 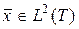 поставим в соответствие вектор
поставим в соответствие вектор 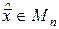 , наиболее близкий к
, наиболее близкий к 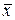 . Таким образом, каждый вектор из
. Таким образом, каждый вектор из 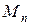 порождает множество эквивалентностей:
порождает множество эквивалентностей:
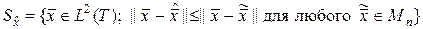 , (1.3.9)
, (1.3.9)
при этом все векторы из 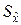 будут иметь одно и то же представление в виде набора
будут иметь одно и то же представление в виде набора 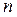 чисел, совпадающее с представлением вектора
чисел, совпадающее с представлением вектора 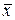 .
.
Важное значение в теории сигнала имеет теорема проектирования, утверждающая, что для любого вектора 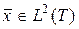 существует единственный вектор
существует единственный вектор 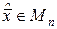 , задаваемый разложением
, задаваемый разложением
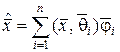 , (1.3.10)
, (1.3.10)
такой, что разность 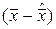 ортогональна ко всем векторам из
ортогональна ко всем векторам из 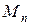 и
и 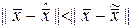 , где
, где 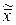 -любой другой вектор из
-любой другой вектор из 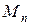 .
.
Докажем это.
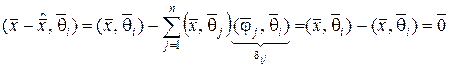 . (1.3.11)
. (1.3.11)
Отсюда следует, что вектор 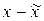 ортогонален ко всем векторам в
ортогонален ко всем векторам в 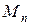 . Для того, чтобы показать, что
. Для того, чтобы показать, что 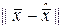 - минимальная из всех
- минимальная из всех 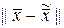 , рассмотрим произвольный вектор
, рассмотрим произвольный вектор 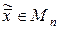 :
:
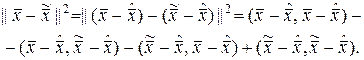 (1.3.12)
(1.3.12)
Поскольку т.к. 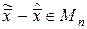 , средние слагаемые пропадают, и мы имеем
, средние слагаемые пропадают, и мы имеем
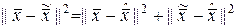 , (1.3.13)
, (1.3.13)
откуда следует, что минимум достигается при 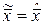 .
.
Вектор 
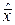 называют ортогональной проекцией вектора
называют ортогональной проекцией вектора 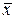 на
на 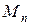 , а вектор
, а вектор 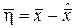 погрешностью приближения вектора
погрешностью приближения вектора 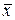 вектором
вектором 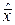 .
.
Дата добавления: 2016-11-04; просмотров: 1592;