Полные ортонормальные системы
Рассмотрим вопрос о сходимости представления произвольного сигнала в конечномерном пространстве 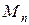 . Будем предполагать, что число измерений подпространства можно произвольно увеличивать. (При этом вопросы оптимальности подпространств, натянутых на базисные функции, рассмотрены не будут).
. Будем предполагать, что число измерений подпространства можно произвольно увеличивать. (При этом вопросы оптимальности подпространств, натянутых на базисные функции, рассмотрены не будут).
Пространство 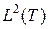 - полное сепарабельное пространство, т.е. выбирая
- полное сепарабельное пространство, т.е. выбирая 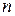 достаточно большим, можно получить сколь угодно близкую аппроксимацию любого
достаточно большим, можно получить сколь угодно близкую аппроксимацию любого 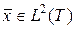
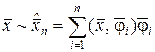 , (1.3.16)
, (1.3.16)
где 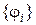 - бесконечное множество ортонормированных функций, для которых
- бесконечное множество ортонормированных функций, для которых
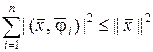 . (1.3.17)
. (1.3.17)
Соотношение (1.70) есть неравенство Бесселя, оно показывает, что сумма квадратов коэффициентов разложения 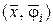 ограничена для любого
ограничена для любого 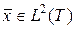 .
.
Неравенство Бесселя вытекает из следующих соображений:
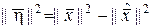 ,
,
где 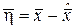 .
.
При 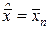
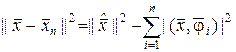 .
.
Отсюда же следует, что 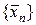 - последовательность Коши, сходящаяся в пространстве
- последовательность Коши, сходящаяся в пространстве 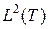 к некоторой точке. Если
к некоторой точке. Если 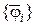 - полная ортонормированная система, то
- полная ортонормированная система, то 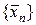 сходится к
сходится к 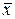 . Ортонормированная система является полной, если не существует дополнительных, отличных от нуля ортогональных векторов, которые можно было бы добавить к системе.
. Ортонормированная система является полной, если не существует дополнительных, отличных от нуля ортогональных векторов, которые можно было бы добавить к системе.
Заметим, что произвольная бесконечная ортонормальная система не обязательно полная. В частности, система функций из теоремы Котельникова
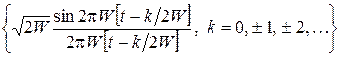
ортонормальная, но не полная в 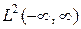 , т.к. функции с частотой больше
, т.к. функции с частотой больше 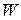 не принадлежат подпространству, натянутому на эту систему. Не нужно путать полноту метрического пространства и полноту ортонормальной системы.
не принадлежат подпространству, натянутому на эту систему. Не нужно путать полноту метрического пространства и полноту ортонормальной системы.
Для полной ортонормальной системы неравенство Бесселя превращается в равенство
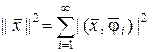 для любого
для любого 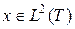 .
.
Таким образом, выбирая 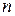 достаточно большим для
достаточно большим для 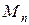 , можно норму погрешности сделать сколь угодно малой. При этом, правда, для разных
, можно норму погрешности сделать сколь угодно малой. При этом, правда, для разных 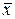 будет разное
будет разное 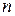 . Тем не менее, такое представление очень широко используется, так как:
. Тем не менее, такое представление очень широко используется, так как:
1. Скалярное произведение в 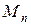 и
и 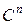 совпадают;
совпадают;
2. Известно много ортонормальных систем;
3. Если известна проекция 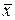 на
на 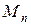 , то для нахождения проекции на
, то для нахождения проекции на 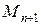 не нужно производить все вычисления заново, а достаточно определить
не нужно производить все вычисления заново, а достаточно определить 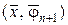 (благодаря самосопряженности базиса), т.е. каждый
(благодаря самосопряженности базиса), т.е. каждый 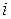 -ый член разложения – это частная проекция на одномерное пространство.
-ый член разложения – это частная проекция на одномерное пространство.
При определении базисных функций для представления сигнала часто используют понятие нормы с весом. При оценке погрешности представления бывает желательно обратить внимание на какой-либо участок области определения функции. Для этого используют интеграл
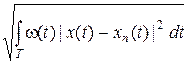 , (1.3.18)
, (1.3.18)
где 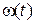 - некоторая неотрицательная функция, определенная на отрезке
- некоторая неотрицательная функция, определенная на отрезке 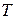 , вместо нормы
, вместо нормы 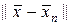 .
.
Интеграл
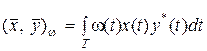 (1.3.19)
(1.3.19)
удовлетворяет условиям для скалярного произведения, а система функций 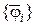 ортонормальна с весом
ортонормальна с весом 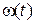 , если
, если 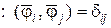 . При этом базисные функции претерпевают лишь незначительные изменения:
. При этом базисные функции претерпевают лишь незначительные изменения:
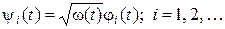 , (1.3.20)
, (1.3.20)
где 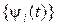 ортонормальны в обычном смысле, а
ортонормальны в обычном смысле, а 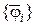 - с весом
- с весом 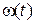 .
.
Дата добавления: 2016-11-04; просмотров: 2235;











