Примеры полных ортонормальных функций
Приведем несколько примеров ортонормальных систем функций, используемых для представления сигналов с заданными областью определения 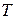 и весовой функцией
и весовой функцией 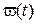 .
.
1. Комплексные гармонические функции
Для комплексных гармонических функций 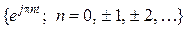
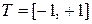 и
и 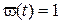 , функции уже ортогональны (указать на пример, где будет искаться взаимный базис), следовательно, для получения ортонормальной системы их нужно нормировать, то есть поделить на норму соответствующей функции ряда. Найдем эту норму
, функции уже ортогональны (указать на пример, где будет искаться взаимный базис), следовательно, для получения ортонормальной системы их нужно нормировать, то есть поделить на норму соответствующей функции ряда. Найдем эту норму
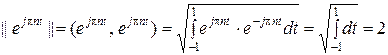 .
.
Представление сигнала с помощью ???
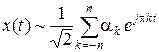 , (1.3.21)
, (1.3.21)
где
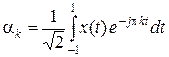
это представление рядом Фурье функций, которые ограниченны на отрезке 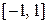 или периодические с периодом, равным 2. Однако это представление применимо для функций, заданных на любом конечном интервале, который можно привести к интервалу
или периодические с периодом, равным 2. Однако это представление применимо для функций, заданных на любом конечном интервале, который можно привести к интервалу 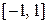 выбором подходящего масштаба по оси времени.
выбором подходящего масштаба по оси времени.
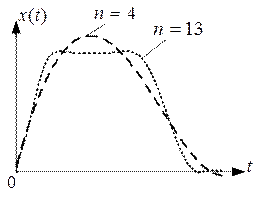
Рассмотрим пример. Пусть требуется с помощью гармонических функций представить сигнал, приведенный на рис.
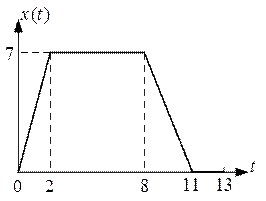
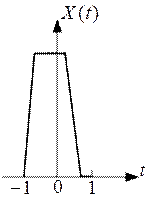
Задан трапецевидный сигнал 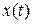 на интервале
на интервале 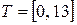 (рис. 1):
(рис. 1):
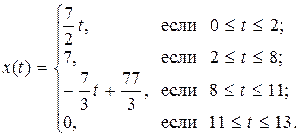
Необходимо представить его рядом комплексных гармонических функций, то есть в виде
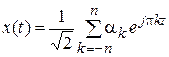 .
.
Комплексные гармонические функции 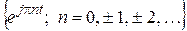 определены на интервале
определены на интервале 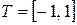 , следовательно, и исходный сигнал должен быть задан на этом же интервале. Для этого подвергнем его сжатию в
, следовательно, и исходный сигнал должен быть задан на этом же интервале. Для этого подвергнем его сжатию в 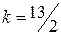 раза, а затем произведем сдвиг на
раза, а затем произведем сдвиг на 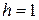 влево. Новый сигнал будет описываться формулой
влево. Новый сигнал будет описываться формулой 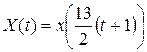 .
.
Коэффициенты разложения найдем по формуле
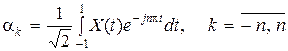 .
.
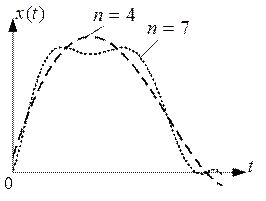
Затем переходим к исходному масштабу и получаем аппроксимированный исходный сигнал. Графики для различных 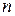 приведены на рис. 2.
приведены на рис. 2.

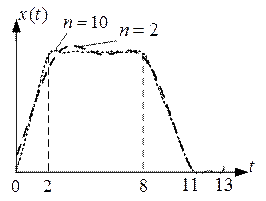
2. Полиномы Лежандра
Для 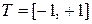 и
и 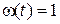 можно получить другую ортонормальную систему, применив процедуру Грама-Шмидта к последовательности
можно получить другую ортонормальную систему, применив процедуру Грама-Шмидта к последовательности 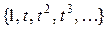 (указать, где мы это сделали). В результате получаются нормированные полиномы:
(указать, где мы это сделали). В результате получаются нормированные полиномы:
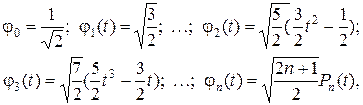 (1.3.22)
(1.3.22)
где 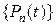 - полиномы Лежандра. Эти полиномы можно также считать по формуле
- полиномы Лежандра. Эти полиномы можно также считать по формуле
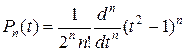 (1.3.23)
(1.3.23)
или по рекуррентной формуле
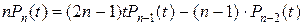 . (1.3.24)
. (1.3.24)
Полином 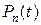 имеет
имеет 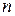 нулей, все они вещественны и находятся в интервале
нулей, все они вещественны и находятся в интервале 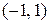 .
.
Разложим рассмотренный выше сигнал. Коэффициенты разложения найдем по формуле
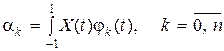 .
.
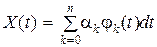
Аппроксимированный сигнал представлен на рис.

3. Полиномы Чебышева
Для 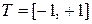 и
и 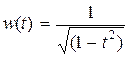 полиномы
полиномы
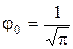
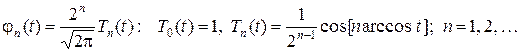 (1.3.25)
(1.3.25)
где 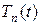 - полиномы Чебышева образуют ортонормальную систему.
- полиномы Чебышева образуют ортонормальную систему.
Для 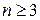
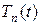 удовлетворяют рекуррентной формуле
удовлетворяют рекуррентной формуле
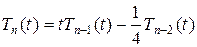 . (1.3.26)
. (1.3.26)
Свойствополиномов Чебышева: из всех полиномов 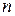 -ой степени, имеющих коэффициент при
-ой степени, имеющих коэффициент при 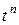 , равный 1,
, равный 1, 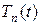 на интервале
на интервале 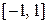 наименее отклоняются от нуля.
наименее отклоняются от нуля.
Без весовой функции
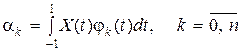 .
.

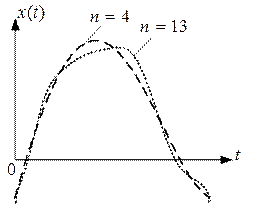
С весовой функции
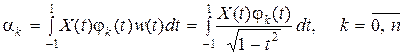 .
.

4. Функции Лагерра
Для 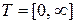 и
и 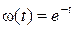 полиномы
полиномы
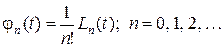 (1.3.27)
(1.3.27)
образуют ортонормальную систему. Здесь 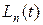 - полиномы Лагерра, задаваемые формулой
- полиномы Лагерра, задаваемые формулой
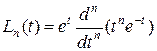 . (1.3.27)
. (1.3.27)
Они имеют 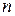 вещественных нулей на
вещественных нулей на 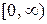 и удовлетворяют рекуррентному соотношению
и удовлетворяют рекуррентному соотношению
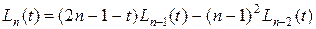 . (1.3.28)
. (1.3.28)
Функции Лагерра имеют единичный вес и ортонормальны на 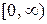
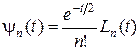 .
.
Они также могут быть получены применением процедуры Грама-Шмидта к последовательности 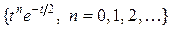 . Функции Лагерра могут быть реализованы практически как импульсные реакции сравнительно простых физических цепей конечного порядка. Для этого их записывают как
. Функции Лагерра могут быть реализованы практически как импульсные реакции сравнительно простых физических цепей конечного порядка. Для этого их записывают как
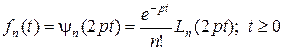 . (1.3.29)
. (1.3.29)
Функции 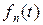 имеют преобразование Лапласа вида
имеют преобразование Лапласа вида
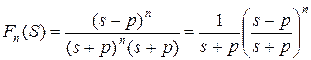 , (1.3.30)
, (1.3.30)
откуда видно, что 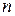 -ая функция Лагерра - это импульсная реакция цепи, один каскад которой имеет передаточную функцию
-ая функция Лагерра - это импульсная реакция цепи, один каскад которой имеет передаточную функцию 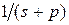 , а
, а 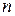 последующих одинаковы с функцией
последующих одинаковы с функцией 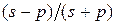 , т. е. это фазовращатели, не изменяющик энергию сигнала. Это так называемый «трансверсальный» фильтр, импульсная реакция которого есть произвольная линейная комбинация функций Лaгерра.
, т. е. это фазовращатели, не изменяющик энергию сигнала. Это так называемый «трансверсальный» фильтр, импульсная реакция которого есть произвольная линейная комбинация функций Лaгерра.
5. Функции Лежандра
Подстановка 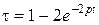 преобразует интервал
преобразует интервал 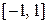 для величины
для величины 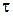 в интервал
в интервал 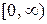 для величины
для величины 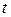 , поэтому из полиномов Лежандра можно получить еще одну систему функций, ортонормальных на
, поэтому из полиномов Лежандра можно получить еще одну систему функций, ортонормальных на 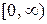 (
( 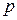 - произвольный дествительный положительный параметр). Функции Лежандра
- произвольный дествительный положительный параметр). Функции Лежандра
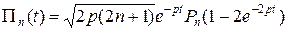 . (1.3.31)
. (1.3.31)
Образуют ортонормальную систему на 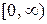 с единичным весом. Преобразования Лапласа от этих функций имеют полюсы при
с единичным весом. Преобразования Лапласа от этих функций имеют полюсы при 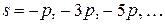
6. Функции Чебышева
Преобразованием 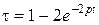 Чебышева получаем функции
Чебышева получаем функции
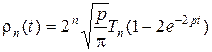 , (1.3.32)
, (1.3.32)
которые ортонормальны с весом 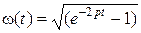 на
на 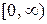 . Полюсы преобразования Лапласа получаются при
. Полюсы преобразования Лапласа получаются при 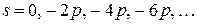
7. Функции Эрмита
Для 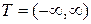 и
и 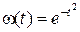 полиномы
полиномы
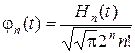 (1.3.33)
(1.3.33)
образуют ортонормальную систему. 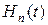 - полиномы Эрмита, которые задаются в виде
- полиномы Эрмита, которые задаются в виде
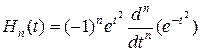 (1.3.34)
(1.3.34)
или рекуррентной формулой
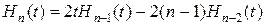 . (1.3.35)
. (1.3.35)
Функций Эрмита
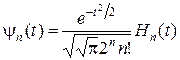 (1.3.36)
(1.3.36)
ортонормальны с единичным весом на 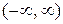 и могут быть получены процедурой Грама-Шмидта к последовательности
и могут быть получены процедурой Грама-Шмидта к последовательности 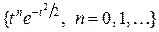 .
.
8. Функции Уолша
Для 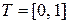 и
и 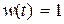 можно построить полную ортонормальную систему функций типа типа «прямоугольных волн». Каждая
можно построить полную ортонормальную систему функций типа типа «прямоугольных волн». Каждая 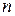 -ая функция содержит
-ая функция содержит 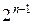 прямоугольных волн, поэтому в обозначении функции удобно использовать два индекса:
прямоугольных волн, поэтому в обозначении функции удобно использовать два индекса: 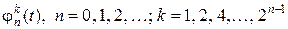 .
.
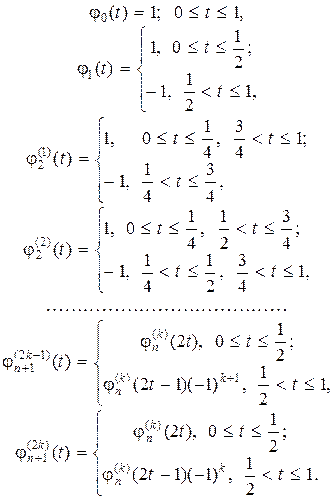 (1.3.37)
(1.3.37)
Эта система важна для практики, поскольку функции кусочно-постоянны и принимаю лишь два значения ( 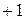 или
или 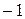 ). Подобные сигналы могут быть легко получены с помощью двоичных логических схем. Перемножение таких сигналов для получения, скажем, скалярного произведения производится очень просто, с помощью ключа, изменяющего полярность и включаемого в нужные моменты времени. Заметим, что функции
). Подобные сигналы могут быть легко получены с помощью двоичных логических схем. Перемножение таких сигналов для получения, скажем, скалярного произведения производится очень просто, с помощью ключа, изменяющего полярность и включаемого в нужные моменты времени. Заметим, что функции 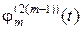 соответствуют обычным прямоугольным волнам. Мы можем перейти к соответствующей одноиндексной системе, упорядочив функции (1.3.37) так, чтобы
соответствуют обычным прямоугольным волнам. Мы можем перейти к соответствующей одноиндексной системе, упорядочив функции (1.3.37) так, чтобы 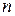 -ая функция
-ая функция 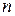 раз пересекала нулевой уровень на интервале
раз пересекала нулевой уровень на интервале 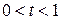 (т.е.
(т.е. 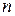 раз меняла знак). Это достигается при следующих обозначениях:
раз меняла знак). Это достигается при следующих обозначениях:
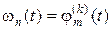 , (1.3.38)
, (1.3.38)
где 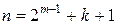 (рис. 1.8).
(рис. 1.8).

Функции Уолша определены на интервале 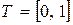 , следовательно, и исходный сигнал
, следовательно, и исходный сигнал 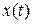 должен быть задан на этом же интервале. Для этого подвергнем его сжатию в
должен быть задан на этом же интервале. Для этого подвергнем его сжатию в 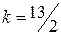 . Новый сигнал будет описываться формулой
. Новый сигнал будет описываться формулой 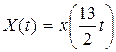 .
.
Коэффициенты разложения найдем по формуле
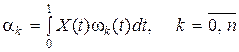 .
.
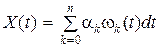 .
.


Дата добавления: 2016-11-04; просмотров: 1889;











