Метрические пространства сигналов
После объединения различных, но обладающих каким-то общим свойством, сигналов в одно множество нас начинают интересовать отличающиеся свойства отдельных элементов этого множества. Вызвано это тем, что каждый сигнал представляет интерес лишь в сравнении его с другими сигналами этого множества. Например, нас может интересовать амплитуда, энергия или длительность сигнала по сравнению с аналогичными параметрами других сигналов.
Общий подход для исследования различий между сигналами множества состоит в том, что каждой паре сигналов ставится в соответствие действительное положительное число, которое трактуется как расстояние между сигналами. После этого множество приобретает геометрические свойства.
Это равносильно введению функционала 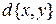 , отображающего все пары сигналов множества на действительную ось
, отображающего все пары сигналов множества на действительную ось 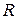
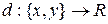 .
.
Функционал 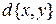 называется метрикой и обладает следующими свойствами:
называется метрикой и обладает следующими свойствами:
а) 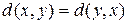 (свойство симметрии);
(свойство симметрии);
б) 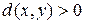 при
при 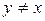 и
и 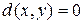 при
при 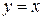 (не отрицательность); (1.2.1)
(не отрицательность); (1.2.1)
в) 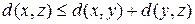 (неравенство треугольника).
(неравенство треугольника).
Свойство а) отражает симметрию, свойство б) говорит о том, что расстояние не может быть отрицательным, свойство в) называют неравенством треугольника: длина одной стороны треугольника не может быть больше суммы длин двух других сторон (представляя точки 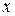 ,
, 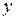 и
и 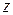 как вершины треугольника).
как вершины треугольника).
Множество сигналов с подходящим образом определенным расстоянием представляет собой пространство сигналов.
Если множество обладает некоторой метрикой 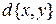 , то оно называется метрическим пространством
, то оно называется метрическим пространством 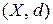 . Например, действительная ось
. Например, действительная ось 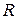 является метрическим пространством с метрикой
является метрическим пространством с метрикой
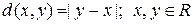 . (1.2.2)
. (1.2.2)
Эту метрику называют обычной метрикой. Часто используют и другие метрики. Например, если 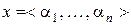 ,
, 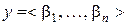 являются упорядоченными множествами (кортежами), то примеры возможных метрик дают следующие функционалы:
являются упорядоченными множествами (кортежами), то примеры возможных метрик дают следующие функционалы:
а) 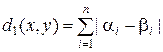 - эту метрику называют манхеттовым расстоянием;
- эту метрику называют манхеттовым расстоянием;
б) 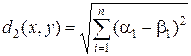 - эту метрику называют евклидовым расстоянием; (1.2.3)
- эту метрику называют евклидовым расстоянием; (1.2.3)
в) 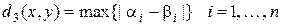 .
.
Метрика б), в частности, используется для комплексных чисел: модуль числа 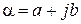 равен
равен 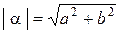 .
.
Приведем пример еще одной метрики, используемой для последовательностей двоичных символов, состоящих из нулей и единиц – кодовых слов фиксированной длины. Если слова содержат по 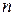 символов, то расстояние между словами можно определить как
символов, то расстояние между словами можно определить как
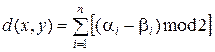 , (1.2.4)
, (1.2.4)
т.е. как сумму несовпадающих символов в одноименных разрядах двоичных слов. Данное расстояние называют расстоянием по Хеммингу и используют, например, в системах связи для обнаружения и исправления ошибочных символов. Для этого заданием расстояния между любой парой слов, равного числу несовпадающих символов, из множества допустимых слов образуется метрическое пространство. Рассмотрим примеры кодов с обнаружением и коррекцией.
Ниже приведены восемь кодов, выбранных из шестнадцати возможных таким образом, чтобы в наборе а) минимальное расстояние между любой парой слов было равно 2.
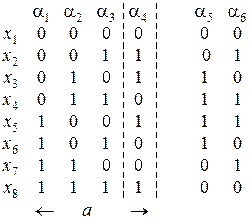
Это может быть достигнуто добавлением к трем информационным разрядам 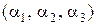 разряда
разряда 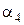 проверки на четность
проверки на четность
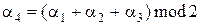 .
.
При этом каждое слово 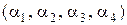 содержит четное число единиц. Поскольку минимальное расстояние между словами равно 2, появление ошибки в одном разряде может быть обнаружено.
содержит четное число единиц. Поскольку минимальное расстояние между словами равно 2, появление ошибки в одном разряде может быть обнаружено.
Если к разрядам 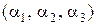 добавить еще разряды проверки на четность
добавить еще разряды проверки на четность 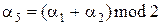 и
и 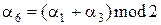 , то получим множество кодовых слов
, то получим множество кодовых слов 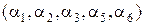 с минимальным расстоянием, равным 3. В этом случае получаем уже корректирующий код, т.к. появление однократной ошибки (т.е. одного ошибочного символа в слове) приводит к получению кода, который ближе к правильному коду, чем ко всем остальным, поскольку отличается от него только на единицу.
с минимальным расстоянием, равным 3. В этом случае получаем уже корректирующий код, т.к. появление однократной ошибки (т.е. одного ошибочного символа в слове) приводит к получению кода, который ближе к правильному коду, чем ко всем остальным, поскольку отличается от него только на единицу.
1.2.2. Сходимость последовательностей сигналов
Рассмотрим свойство бесконечных последовательностей сигналов, которое связано с понятием расстояния и называется сходимостью. Говорят, что последовательность сигналов 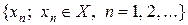 сходится, если существует такое
сходится, если существует такое 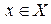 , что для любого
, что для любого 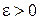 найдется положительное число
найдется положительное число 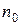 , такое, что при
, такое, что при
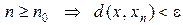 .
.
(Иногда это записывают как: 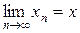 .)
.)
Любая последовательность, обладающая таким свойством, называется последовательностью Коши.
Заметим, что последовательность Коши может не быть сходящейся только потому, что элемент 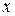 , к которому в пределе стремится последовательность, может не принадлежать множеству
, к которому в пределе стремится последовательность, может не принадлежать множеству 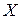 .
.
Если метрическое пространство обладает свойством, что все последовательности Коши в нем являются сходящимися, то оно называется полным.
Дата добавления: 2016-11-04; просмотров: 1791;











