Добавим к целевой функции (8) бюджетные ограничения

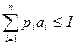, х₁ ≥ 0, … , х_n ≥ 0 получим задачу, называемую моделью Р.Стоуна.

Проведя некоторые преобразования можно получить функцию спроса:

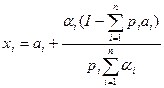
Эту функцию легко интерпретировать. Вначале приобретается минимально необходимое количество каждого блага a_i. Затем рассчитывается сумма денег, оставшаяся после этого, которая распределяется пропорционально «весам» важности α_i. Разделив количество денег на сумму р_i, получаем дополнительно приобретаемое, сверх минимума, количество i – го блага и добавляем его к а_i.

Модель Стоуна имеет различные частные случаи:

Когда все а_i = 0, а все α_i равны между собой, получаем

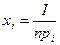
т.е. доход делится на n равных частей и спрос на i – й товар рассчитывается как частное от деления полученной суммы денег на его цену.

Спрос растет при росте дохода с эластичностью, равной единице, и уменьшается с ростом цены с эластичностью, равной минус единице.

Каждый товар в этой модели является нормальным и ценным. Спрос растет до бесконечности при бесконечном росте дохода – в этом смысле каждый товар является «предметом роскоши».

Для того, чтобы описать более разнообразные формы поведения спроса на различные товары, модель должная включать другие, более сложные виды целевой функции предпочтения.

Пример.

При функции предпочтения

U (x₁, x₂) = x₁^a x₂^b-a (x₁ + b – a)^-b ,

где a и b – параметры.

Функция спроса имеет вид:

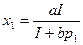- типичная функция спроса для предметов первой необходимости

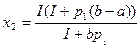- типичная функция спроса для предметов роскоши

2.5 Взаимозаменяемость и взаимодополняемость благ. Эффекты компенсации