Понятие производственной функции.

Производственная функция- это функция, независимая переменная которой принимает значение объёмов затрачиваемого или используемого ресурса (фактора производства), а зависимая переменная значения объёмов выпускаемой продукции:

y= f(x), x≥0, y≥0

x, y- числовые величины, т.е. y= f(x) есть функция одной переменной х. Производственная функция (ПФ) f - называется одноресурсной или однофакторной ПФ, её область определения - множество неотрицательных действительных чисел, т.е. x≥0.

Записьy= f(x) означает, что если ресурс затрачивается или используется в качестве х - единиц, то продукция выпускается в количествеy= f(x)единиц.

Символ f - знак функции, является характеристикой производственной системы, преобразующей ресурс в выпуск.

Символ f связывает между собой независимую переменную х с зависимой переменной у.

В микроэкономической теории принято считать, что у - это максимально возможный объём выпуска продукции, если ресурс затрачивается или используется в количествеxединиц.

В макроэкономической теории такое понятие не совсем корректно: возможно, при другом распределении ресурсов между структурными единицами экономики выпуск мог бы быть и большим.

В этом случае ПФ - это статистически устойчивая связь между затратами ресурса и выпуском.

Более правильной является символика y= f(x,а),где а - вектор параметров ПФ.

3.1 Производственная функция видаf(x)= ах^b

Пример 1:Возьмём ПФ в виде f(x)= ах^b,где а -величина затрачиваемого ресурса (например, рабочего времени), f(x)-объём выпускаемойпродукции (например, число готовых к отправке холодильников).

Величины a и b- параметры ПФ f, здесь a и b- положительные числа и число b≤1, вектор параметров есть двумерный вектор (a,b).

График G производственной функции у = ах^b изображен на рисунке 4.

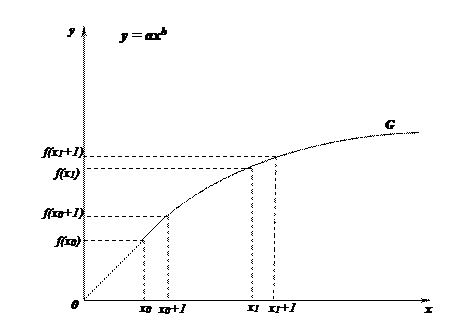
Рис.4.

На графике G производственной функции у = ах^bвидно, что с ростом величины затрачиваемого ресурса х объем выпуска у растет, однако при этом каждая дополнительная единица ресурса дает все меньший прирост объема у выпускаемой продукции.

Отмеченное обстоятельство – рост объема и уменьшение прироста объема у. С ростом величины х – отражает фундаментальное положение экономической теории (хорошо подтвержденное практикой), называемое законом убывающей эффективности.

ПФ у = ах^b является типичным примером широкого класса однофакторных ПФ.

ПФ могут иметь разные области использования.

1. На микроуровне экономики:

ПФ у = ах^b может быть использовано для описания взаимосвязи между величиной затрачиваемого или используемого ресурса х в течении года на отдельном предприятии (фирме) и готовым к выпускам продукции у этого предприятия (фирмы).

В роли производственной системы здесь выступает отдельное предприятие (фирма) ­ – имеем микроэкономическую ПФ (МИПФ).

На микроэкономическом уровне в роли производственной системы может выступать также отрасль, межотраслевой производственный комплекс.

МИПФ строятся и используются в основном для решения задач анализа и планирования, а также задач прогнозирования.

1. ПФ может быть использована для описания взаимосвязи между годовыми затратами труда в масштабе региона или страны в целом и годовым конечным выпуском продукции (или дохода) этого региона или страны в целом.

В роли производственной системы выступает регион или страна, точнее хозяйственная система. В этом случае имеем макроэкономический уровень и макроэкономическую ПФ (МАПФ).

Аналогично МАПФ строятся и активно используются для решения всех трех типов задач – анализа, планирования и прогнозирования.

На микроэкономическом уровне затраты и выпуск могут измеряться как в натуральных, так стоимостных единицах (показателях). Годовые затраты труда могут быть измерены в человеко-часах (натуральный показатель), или в рублях выплачиваемой заработной платы (стоимостной показатель); выпуск продукции может быть представлен в штуках или других натуральных единицах (тоннах, метрах и т.д.) или в виде своей стоимости.

На макроэкономическом уровне затраты и выпуск измеряются как правило в стоимостных показателях и представляют собой стоимостные (ценные) агрегаты, т.е. суммарные величины произведений объемов затрачиваемых (или используемых) ресурсов.

Производственная функция нескольких переменных, независимые переменные х₁, …, х_n , которой принимают значения объемов затрачиваемых или используемых ресурсов (число переменных п равно числу ресурсов), а значение функции имеет смысл величин объемов выпуска:

у = f (x) = f (х₁, …, х_n)

y ≥ 0 – скалярная величина, х – векторная величина, х₁, …, х_n – координаты вектора х, т.е. f (х₁, …, х_n) – функция числовая нескольких (многих) переменных (х₁, …, х_n).

ПФ f (х₁, …, х_n) – называют многоресурсной или многофакторной ПФ.

Более правильная символика: f (х₁, …, х_n, а), где а – вектор параметров ПФ.

По экономическому смыслу х₁ ≥ 0,… х_n≥ 0, следовательно, областью определения многофакторной ПФ f (х₁, …, х_n) является множество п -мерных векторов х, все координаты х₁, …, х_n, которых неотрицательные числа.

1). Для отдельного предприятия(фирмы),выпускающего однородный продукт, ПФ f (х₁, …, х_n,) может связать объём выпуска в натуральном или стоимостном выражении с затратами рабочего времени по различным видам трудовой деятельности, различных видов сырья, комплектующих изделий, энергии, основного капитала (обычно в натуральных показателях), ПФ такого типа характеризует действующую технологию предприятия (фирмы).

2). При построении ПФ для региона или страны в целом в качестве величины годового выпуска Y (объём выпуска, или дохода) чаще берут совокупный продукт (доход) региона или страны, исчисляемый обычно в неизменных, а не текущих ценах, в качестве ресурсов рассматривают основной капитал.

х₁ = К – объём используемого в течении года основного капитала;

Живой труд:

х₂ = L- количество единиц затрачиваемого в течении года живого труда, исчисляемые обычно в стоимостном выражении.

Таким образом, строим двухфакторную ПФ f (х₁, ,х₂,) или Y= f(K,L).

От двухфакторных ПФ переходим к трехфакторным. В качестве третьего фактора иногда вводят объемы используемых природных ресурсов. Кроме того, если ПФ строится по данным временных рядов, то в качестве особого фактора роста производства может быть включен технический прогресс.

Пусть ПФ у = f (х₁, х₂) называется статистической, если ее параметры и ее характеристика f не зависит от времени t, в тоже время объемы ресурсов и объем выпуска могут зависеть от времени t, т.е. имеем представления в виде временных рядов:

x₁(0), x₁(1),…, x₁(T);

x₂(0), x₂(1),…, x₂(T);

y(0), y(1), …, y(T);

y(t) = f(x₁(t), x₂(t)), здесь t – номер года.

t =0, 1, …, T;

t = 0 – базовый год временного промежутка, охватывающего годы 1, 2, …, Т.