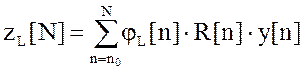Метод аппроксимации
Производственный процесс представлен графически
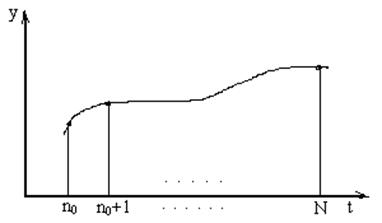
Рис.11.3. График производственного процесса.
y[N+k] - ?
Разложим процесс в ряд:
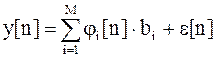 ,
,
где y[n] – отсчеты;
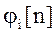 - некоторая система функций, по которой ведём разложение (для тренда это полиномы);
- некоторая система функций, по которой ведём разложение (для тренда это полиномы);
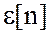 - погрешность измерения (типа «белого шума»);
- погрешность измерения (типа «белого шума»);
bi – искомые коэффициенты.
Модель производственного процесса (аппроксимация) можно представить в виде:
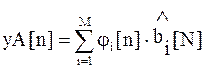 .
.
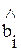 - такие значения, чтобы модель yA[n] была близка к y[n]. Как правило, применяется квадратичный критерий близости.
- такие значения, чтобы модель yA[n] была близка к y[n]. Как правило, применяется квадратичный критерий близости.
Квадратичный критерий имеет вид:
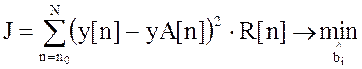 ,
,
здесь подбирается критерий 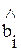 ,
,
R[n] – вес, который мы придаём результатам измерения.
Скользящее стробирование:
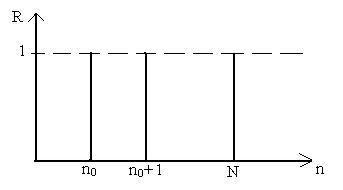
Рис.11.4. Скользящее стробирование.
Экспоненциальное сглаживание (самый распространенный метод):
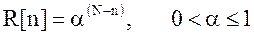
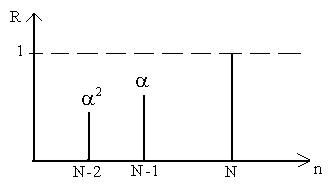
Рис.11.5. Экспоненциальное сглаживание.
Общий случай:
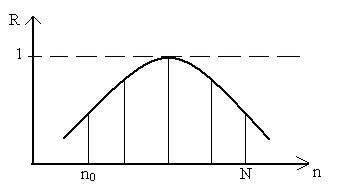
Рис.11.6. Сглаживание функции.
Планирование прогноза – это подбор весовой функции R[n]. Наибольшее распространение получило экспоненциальное сглаживание.
Представим исходный процесс y[n] в матричном виде:
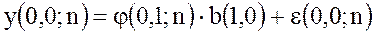 ,
,
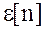 - помеха типа «белого шума» (ошибки между собой не связаны).
- помеха типа «белого шума» (ошибки между собой не связаны).
Это же уравнение можно записать в индексной форме:
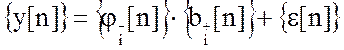 ;
;
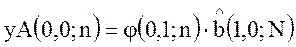 ;
;
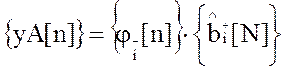 ;
;
условие минимуму этого критерия:
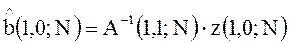 .
.
Элементы матрицы А:
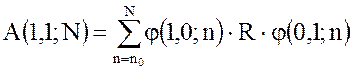 ,
,
в индексной форме:
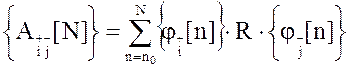 .
.
Уравнение через элементы матриц:
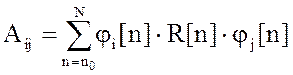 .
.
Матрица z:
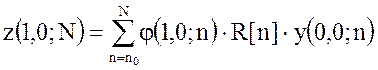 ;
;
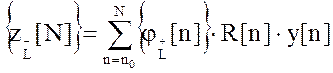 ;
;
|
Дата добавления: 2016-12-09; просмотров: 1417;