Алгоритмы стохастической аппроксимации с ограничениями

Рассмотрим задачу идентификации при наличии ограничения

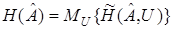(25)

причем вид вектор-функция 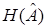неизвестна, а известны лишь реализации вектор-функции .

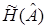Составим функционал

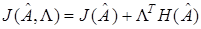
или, учитывая (18), (25),

.

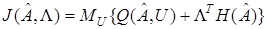Теперь задача свелась к нахождению стационарной точки функционала 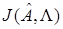по ее реализациям. Для нахождения решения рассматриваемой задачи применим алгоритм (20). Тогда процедура оценивания примет вид

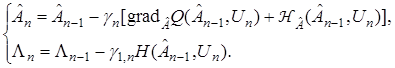(26)

где 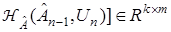— матрица вида

, , .

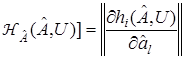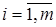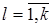Сходимость АСА

Применение любого адаптивного алгоритма возможно только при условии его сходимости к некоторому искомому значению.

В алгоритмы адаптации входит градиент реализации 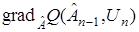. которые зависят от случайного вектора 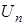. Следовательно, оценки 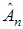также являются случайными и для них непосредственно неприменимо обычное понятие сходимости (устойчивости). Для оценки сходимости алгоритм стохастической аппроксимации применяют соответствующие вероятностные аналоги. Как отмечалось в предыдущей лекции, могут применяться три основных вида такой сходимости: сходимость по вероятности, сходимость в среднеквадратическом и сходимость почти наверное.

Рассмотрим алгоритм (20). Для того чтобы вектор 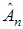стремился к 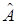почти наверное, необходимо, по крайней мере, чтобы при 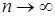второе слагаемое в правой части (20) стремилась к нулю, т. е.

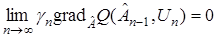для почти 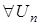. (27)

Так как в общем случае градиент реализации 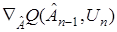отличен нот нуля, то для обеспечения (27) необходимо, чтобы 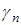с ростом 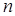стремилось к нулю.

Достаточные условия сходимости алгоритмов адаптации можно сформулировать так. Алгоритм адаптации (20) сходится почти наверное при соблюдении следующих условий:

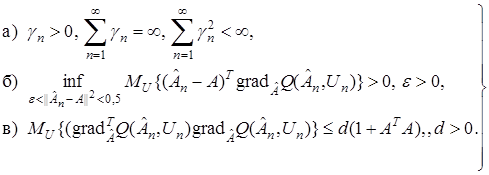(28)

Эти условия имеют весьма простой физический и геометрический смысл.

Условие а) требует, чтобы скорость уменьшения 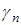была такова, чтобы дисперсия оценки 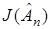уменьшалась до нуля, но чтобы за время изменения 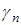можно было использовать достаточно большое число данных, при котором еще справедлив закон больших чисел.

Условие б) определяет характер поведения поверхности 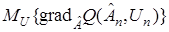вблизи корня, и, следовательно, знаки приращений 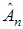. Наконец, условие в) гласит, что математическое ожидание квадратической формы 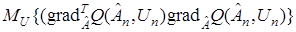с увеличением 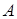должно расти не быстрее квадратичной параболы.

Здесь не будет рассматриваться вопрос о качестве работы алгоритм стохастической аппроксимации, да и других классов адаптивных алгоритмов. Заметим только, они должны минимизировать невязку 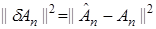. Как это сделать, было показано на примере получения алгоритма Качмажа (14).