Интерполирование функций.

Конечные разности различных порядков.

Пусть 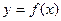- заданная функция. Обозначим через 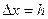фиксированную величину приращения аргумента (шаг). Тогда выражение

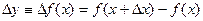(1)

называется первой конечной разностью функции .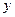

Конечные разности высших порядков

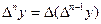
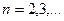
Например,

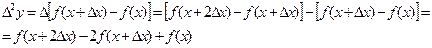
Пример. Построить конечные разности для функции:

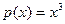, считая шаг .

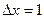Решение:

,

.

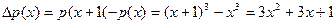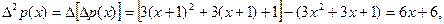
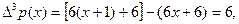
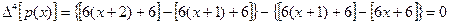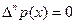, при .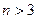

Если 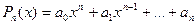- полином n-ой степени, то

(*)

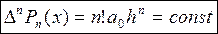где .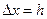

Символ 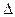можно рассматривать как оператор, ставящий в соответствие функции 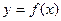функцию .

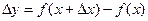Основные свойства оператора :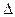

1)

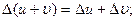
2) 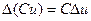, где ;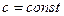

3) .

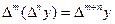Имеет место важная формула, которая может быть получена на основе свойств 1-3.

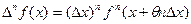, (2)

где 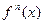- производная (непрерывная) на отрезке , .

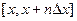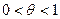Из (2) следует.

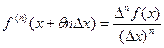
Переходя к пределу и предполагая, что 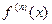непрерывна, получаем

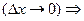
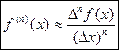- формула для приближенного вычисления производных.

Таблица разностей.

Часто таблицы задаются для системы равноотстоящих точек

.

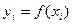
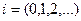
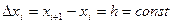Конечные разности определяются соотношениями:

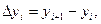
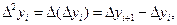
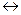в силу свойства 1):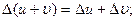

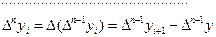
В общем виде можно записать:

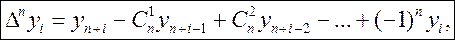(1)

где 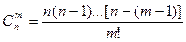- число сочетаний из n элементов по m.

Например: ,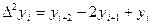

,

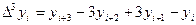и т.д.

Для вычисления n-ой разности 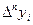, нужно знать n+1 членов 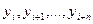последовательности.

Конечные разности различных порядков удобно располагать в форме таблиц двух видов:

Горизонтальная таблица разностей. Диагональная таблица разностей.

…..	…..	…..	…..	…...

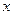
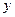
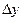
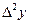
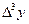
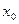
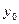
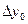
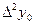
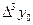
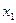
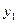
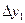
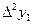
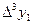
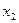
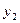
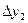
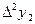
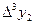
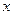
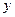
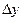
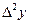
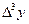
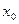
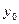
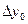
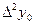
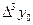
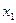
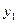
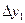
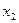
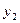
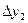
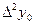
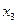
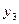
Пример: Составить горизонтальную таблицу разностей функции

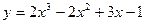
от начального значения 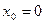, приняв шаг .

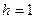Решение: Полагая 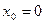, , 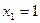, 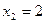находим , , .

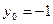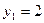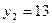Отсюда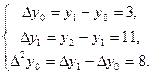

Т.к. n=3 – степень полинома, то 3-и разности .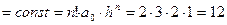

Заносим полученные значения в таблицу (горизонтальную).

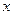
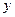
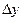
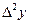
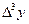
	-1

Исходные данные для заполнения таблицы отмечены ступенчатой ломаной.

Остальные клетки можно заполнить с помощью формул

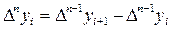
отсюда: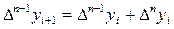

,

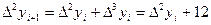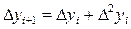и т.д.

,

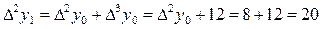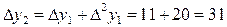и т.д.