Метод интегрируемой аппроксимации

Основная идея метода состоит в подборе аналитической функции, аппроксимирующей нелинейную ВАХ, которая бы позволила произвести расчет переходного процесса в аналитической форме. Рассмотрим метод на конкретном примере.

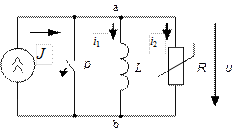Пример 14. Требуется найти закон изменения напряжения u(t) при размыкании рубильника в цепи, схема которой приведена на рис.67, если ВАХ нелинейного резистора задана аналитически функцией 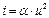, а начальные условия .

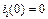Рис.67. Схема цепи

Решение. По первому закону Кирхгофа запишем уравнение:

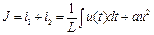. (90)

Продифференцируем его:

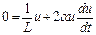, откуда 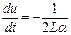. (91)

После разделения переменных и интегрирования получаем:

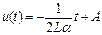, (91)

где А-постоянная интегрирования.

Постоянную интегрирования найдем из начальных условий. После размыкания рубильника при :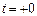

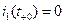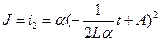, => , (92)

откуда 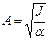. В итоге получаем:

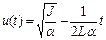. (93)

Из приведенного примера следует, что для нахождения решения в аналитической форме необходимо выбрать аппроксимирующую функцию так, чтобы получаемые уравнения можно было проинтегрировать. При этом не всегда удается добиться достаточной точности расчета, а в некоторых случаях аналитическое решение может не только количественно, но и качественно отличаться от экспериментальных результатов.