Нахождение корней методом половинного деления
Пусть дано уравнение f(x)=0, (1)
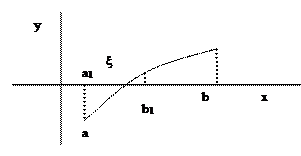 Причем f(x) непрерывна на отрезке [a, b] и
Причем f(x) непрерывна на отрезке [a, b] и 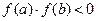 . Делим отрезок пополам и находим середину
. Делим отрезок пополам и находим середину 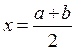
Если f(x1) ≠0 то для продолжения вычисления выберем ту из частей данного отрезка [a, х1] или [х1, b]. Концы нового отрезка обозначим через a1 и b1 .
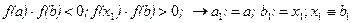
Продолжаем процесс пока не получим либо точный корень уравнения (1) либо не достигнуто значение с заданной точностью. Для оценки точности используется соотношение:
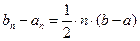 (2)
(2)
Из (2) получаем:
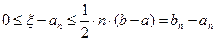 (3)
(3)
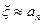 с погрешностью ε не превышающей
с погрешностью ε не превышающей 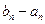
Пример:
Методом половинного деления с точностью ε = 10-2 найти корень уравнения
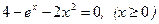
- Определяем корни уравнения при
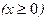
| x | 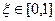 +1 +1
| |
| f(x) | + | - |
- Уточняем значение корня:
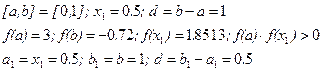
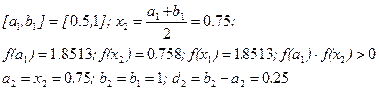
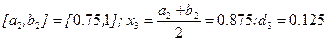
 и т.д.
и т.д.
Заданная точность достигается на седьмом шаге.
х7 =0.8828125 с погрешностью d7=0,0078125<ε=0.01
Блок – схема решения уравнения f(x) методом половинного деления
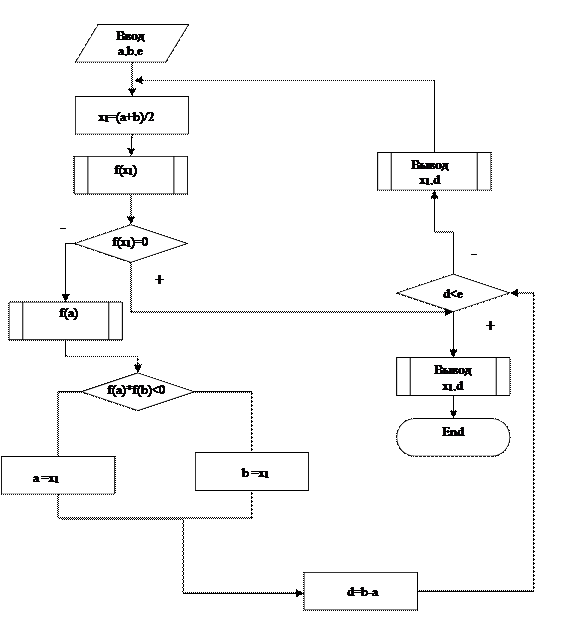
Метод хорд
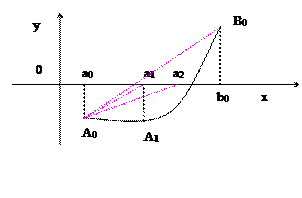 Дано уравнение f(x)=0. Пусть найден отрезок
Дано уравнение f(x)=0. Пусть найден отрезок 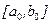 , такой, что на его концах функция f(x) имеет разные знаки, то есть
, такой, что на его концах функция f(x) имеет разные знаки, то есть 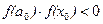 . Пусть, кроме этого, производные
. Пусть, кроме этого, производные 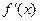 и
и 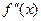 на отрезке
на отрезке 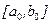 сохраняют знак. (Пусть
сохраняют знак. (Пусть 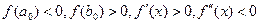 при a0<x<b0).
при a0<x<b0).
За приближенное значение корня принимаем точку пересечения с осью ОХ хорды, проходящей через точки A0[a0,f(a0)], B0[b0,f(b0)]
Уравнение хорды:
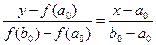 (1)
(1)
Точка пересечения a1 с осью ОХ находится из (1) при у=0 (при этом х=а1):
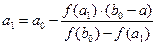 (2)
(2)
Принимая а1 за конец первого отрезка 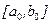 , можно снова провести хорду и получится приближенное значение а2
, можно снова провести хорду и получится приближенное значение а2
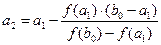 (3)
(3)
И так далее
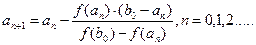 (4)
(4)
Можно показать, что процесс сходится и в пределе 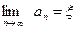 .
.
Метод Ньютона
Пусть ξ – корень уравнения f(x)=0 определен на отрезке 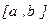 причем
причем 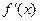 и
и 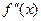 непрерывны и сохраняют знаки при a<x<b. Найдя какое-нибудь n-ое приближенное значение корня xn= ξ (a≤xn≤b), мы можем уточнить его по методу Ньютона.
непрерывны и сохраняют знаки при a<x<b. Найдя какое-нибудь n-ое приближенное значение корня xn= ξ (a≤xn≤b), мы можем уточнить его по методу Ньютона.
Положим
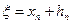 (1)
(1)
Где hn-малая величина.
По формуле Тейлора, беря только линейные члены находим:
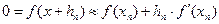 (2)
(2)
Так как 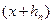 - «корень», то
- «корень», то 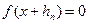
Из (2) следует:
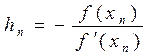
Подставляя hn в (1), получаем новое приближение корня:

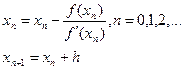 (3)
(3)
Так как уравнение касательной в точке Bn[bn,f(bn)]:
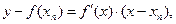
Полагая у=0 (корень!); xn=xn+1 получим
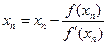
Поэтому метод Ньютона называют еще методом касательных.
Если в качестве начального приближения выбрать точку а, то получили бы новое приближение, выходящее за интервал 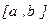 . Следовательно «хорошим» начальным приближением x0 является то, для которого выполнено неравенство:
. Следовательно «хорошим» начальным приближением x0 является то, для которого выполнено неравенство:
 (4)
(4)
Для оценки точности (погрешности) n-го приближения xn можно воспользоваться следующим соотношением:
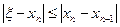 ,
,
 То есть «установившееся» начальные десятичные знаки приближения xn и xn+1,являются верными (следует взять более двух последующих приближений!)
То есть «установившееся» начальные десятичные знаки приближения xn и xn+1,являются верными (следует взять более двух последующих приближений!)
Пример:
Вычислить методом Ньютона отрицательный корень уравнения:
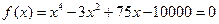
с пятью верными знаками.
Решение:
Полагая х=0,-10,-100,…, получим f(0)=-10000, f(-10)=-1050, f(-100)≈108
Искомый корень находится в интервале [-100,-10]. Сузим интервал, рассматривая точку х=-11 f(-11)=3453.
Таким образом -11<ξ<-10
На этом интервале 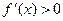 и
и 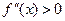 . Так как
. Так как 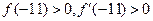 , то есть
, то есть 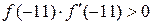 , за начальное приближение выбираем х0=-11.
, за начальное приближение выбираем х0=-11.
Результаты вычислений сводим в таблицу:
| n | xn | f(xn) | 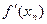
| 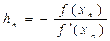
|
| -11 | -5183 | 0.7 | ||
| -10.3 | 134.3 | -4234 | 0.03 | |
| -10.27 | 37.8 | -4196 | 0.009 | |
| -10.261 | 0.2 | - | - |
Останавливаемся на n=3. проверяем точность решения, давая приращение 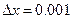 . (два знака до запятой, три знака – после)
. (два знака до запятой, три знака – после)
-5 значащих цифр.
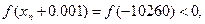
-10261<ξ<-10260
Любое из этих чисел дает искомое приближение. (А хорошо бы еще 1-2 итерации выполнить)
ЛЕКЦИЯ 7
Приближенное решение алгебраических и трансцендентных уравнений (продолжение)
Метод итераций
(метод последовательных приближений)
Пусть дано уравнение:
f(x)=0 (1)
где f(x) – непрерывная функция. требуется вычислить действительный корень уравнения (1) находящийся на отрезке 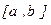 .
.
Заменим уравнение (1) на равносильным ему уравнением
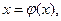 (2)
(2)
где 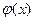 - непрерывна на
- непрерывна на 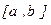 функция.
функция.
Выбираем произвольное 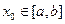 и подставляем его в правую часть равенства (2). Получаем
и подставляем его в правую часть равенства (2). Получаем
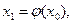
Аналогично получаем
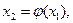
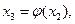
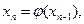
Рассмотрим последовательность x0,x1,x2,…,xn,…
Пусть эта последовательность сходится, то есть существует предел 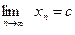 . Покажем, что с – корень уравнения (2) По построению
. Покажем, что с – корень уравнения (2) По построению 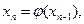 причем
причем 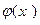 - непрерывная функция. Переходя к пределу при
- непрерывная функция. Переходя к пределу при 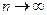 , получаем
, получаем 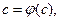 что и требовалось доказать.
что и требовалось доказать.
Так как уравнения (1) и (2) равносильны, то c-корень и уравнения (1), то есть исходного уравнения.
Выясним при каких значениях процесс сходится.
Теорема
Пусть функция 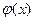 определена и дифференцируема на отрезке
определена и дифференцируема на отрезке 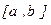 , причем все ее значения
, причем все ее значения 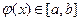 . Пусть кроме этого,
. Пусть кроме этого,
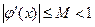 при
при 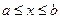 (3)
(3)
Тогда итерационный процесс сходится и дает в пределе единственный корень уравнения 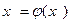
Доказательство:
Уравнение 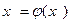 имеет на отрезке
имеет на отрезке 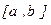 действительный корень. Обозначим его ξ
действительный корень. Обозначим его ξ
Выбираем произвольные 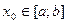 и строим итерационную последовательность
и строим итерационную последовательность 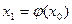 ;
; 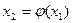 ;…;
;…; 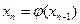 .
.
Рассмотрим уравнение
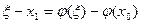 . (*)
. (*)
Т.к. ( 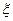 - корень уравнения
- корень уравнения 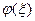 , т.е.
, т.е. 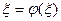 , а
, а 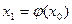 ).
).
Применяем теорему Лагранжа к уравнению (*).
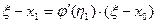 ,
,
где 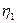 лежит между
лежит между 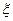 и
и 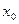 , т.е.
, т.е. 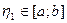 .
.
Согласно неравенству (3), имеем
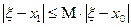 , т.к.
, т.к. 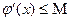 .
.
Аналогично находим
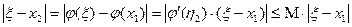
Используя следующее неравенство, получаем
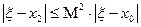
Повторяя процесс, получаем
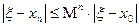 (4)
(4)
По условию теоремы 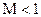 , поэтому из (4) следует
, поэтому из (4) следует
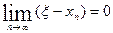 , т.е.
, т.е. 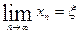 .
.
Т.е. итерационная последовательность сходится и дает в пределе корень уравнения 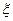 . Корень этот единственный.
. Корень этот единственный.
Действительно, предположим, что на этом отрезке есть еще корень уравнения 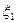 . Тогда
. Тогда 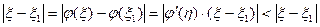 т.к.
т.к. 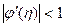 .
.
Пришли к противоречию. Теорема доказана.
Замечание 1. По условию теоремы итерационный процесс сходится при любом выборе 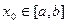 . Благодаря этому он является самоисправляющимся, т.к. неверно вычисленное
. Благодаря этому он является самоисправляющимся, т.к. неверно вычисленное 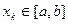 можно рассматривать как новое нулевое приближение.
можно рассматривать как новое нулевое приближение.
Замечание 2. 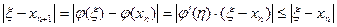 ,
, 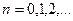
Т.к. 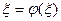 ,
, 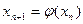 , то каждое последующее приближение ближе к корню чем предыдущее.
, то каждое последующее приближение ближе к корню чем предыдущее.
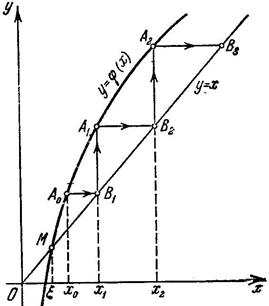
Геометрический смысл метода итераций.
 Корень уравнения
Корень уравнения 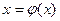 - это абсцисса точки пересечения кривой
- это абсцисса точки пересечения кривой 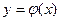 и прямой
и прямой 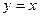 .
.
а) При 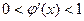 приближения
приближения 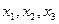 и т.д. монотонно убывают, приближаясь к
и т.д. монотонно убывают, приближаясь к 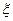 (или возрастают, если
(или возрастают, если 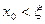 ).
).
Условие теоремы 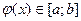 , автоматически выполняются если
, автоматически выполняются если 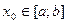 .
.
б) При 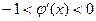 последовательные приближения колеблются около
последовательные приближения колеблются около 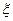 .
.
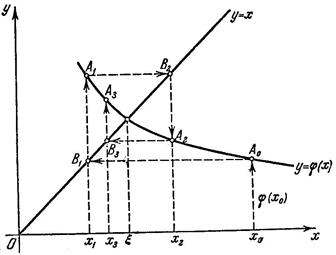
в) При 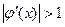 итерационный процесс расходится!
итерационный процесс расходится!
Для применения метода итераций уравнение 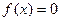 нужно привести к виду
нужно привести к виду 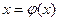 так, чтобы
так, чтобы 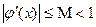 при
при 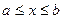 .
.
Это можно сделать различными способами:
1. Уравнение 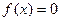 заменяется равносильным
заменяется равносильным 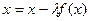 .
.
В этом случае 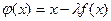 .
.
Параметр подбирают так, чтобы 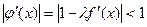 , при
, при 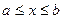 .
.
2. Уравнение 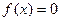 заменяется равносильным
заменяется равносильным 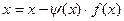 ,
,
где 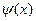 - произвольная, дифференцируемая на отрезке
- произвольная, дифференцируемая на отрезке 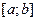 функция, не имеющая корней на отрезке
функция, не имеющая корней на отрезке 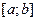 .
.
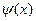 подбирают так, чтобы
подбирают так, чтобы 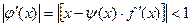 , при
, при 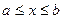 .
.
Можно показать, что при соответствующем выборе функции 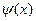 , получаются расчетные формулы метода хорд и метода касательных.
, получаются расчетные формулы метода хорд и метода касательных.
Оценка приближения.
Из условия (4) 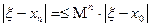 , учитывая, что
, учитывая, что 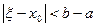 , получаем
, получаем
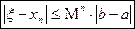 . (1)
. (1)
Приведем без доказательства еще одну формулу для оценки погрешностей.
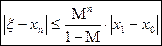 . (2)
. (2)
Из (1) и (2) следует, что итерационный процесс сходится тем быстрее, чем меньше 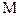 .
.
Если 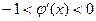 , погрешность удобно оценить так: последовательные приближения
, погрешность удобно оценить так: последовательные приближения 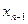 и
и 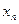 , в этом случае лежат по разные стороны от корня
, в этом случае лежат по разные стороны от корня 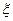 . Поэтому
. Поэтому
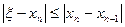 . (3)
. (3)
Если за приближенное значение корня взять полусумму последних полученных приближений 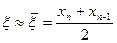 , то
, то 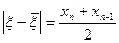 .
.
Пример:Вычислить приближенно действительный корень уравнения.
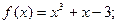
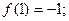
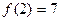 .
.
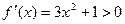 при всех
при всех 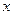 .
.
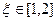 Сузим этот интервал методом половинного деления.
Сузим этот интервал методом половинного деления.
Вычислим 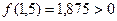 , поэтому
, поэтому 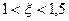 .
.
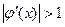 ! поэтому заменяем исходное уравнение равносильным
! поэтому заменяем исходное уравнение равносильным
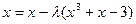 ,
,
получаем 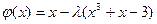 ;
; 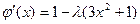 .
.
Находим 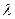 , такое чтобы
, такое чтобы 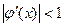 при
при 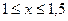 .
.
Пусть 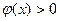
Тогда 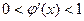
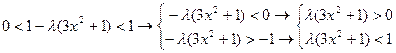
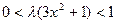
При 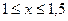 ,
, 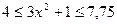
Получаем 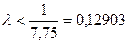 .
.
Пусть 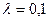
При таком 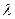 выполняется достаточное условие сходимости итерационного процесса, т.к.
выполняется достаточное условие сходимости итерационного процесса, т.к. 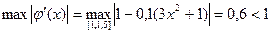 ;
; 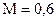 .
.
Выбираем 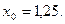
Подставляем 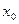 , в правую часть уравнения
, в правую часть уравнения
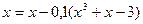
получаем 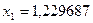
Аналогично находим:
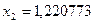 ;
; 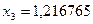 ;
; 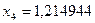 ;
; 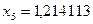 ;
;  ;
; 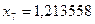 ;
; 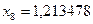 ;
; 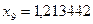 ;
;
Оценим погрешность по формуле 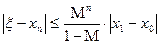
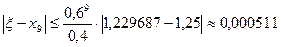
Итак 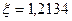 ;
; 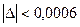
1) Условие сходимости 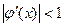 всегда выполняется для функций
всегда выполняется для функций 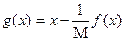 , где
, где 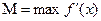
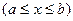 .
.
2) Если производная 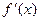 отрицательна на отрезке
отрицательна на отрезке 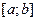 , то уравнение
, то уравнение 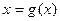 , заменяется на
, заменяется на 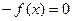 .
.
ЛЕКЦИЯ 8
Дата добавления: 2016-11-04; просмотров: 7855;











