Приближенное решение алгебраических и трансцендентных уравнений

В трансцендентных уравнениях неизвестные входят под знаком трансцендентных функций, то есть неалгебраических, то есть тригонометрических показателей и др.

Пусть дано уравнение

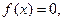(1)

где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале .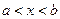

Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0, называется корнем уравнения (1) или нулем функции f(x).

Будем предполагать, что уравнение (1) имеет лишь изолированные корни, то есть для каждого корня уравнения (1) существует окрестность , не содержащая других корней этого уравнения.

Приближенное нахождение изолированных действительных корней уравнения (1) складывается обычно из двух этапов:

1. отделение корней, то есть установление возможно тесных промежутков [α, β], в которых содержится один и только один корень уравнения (1);
2. уточнение приближенных корней, то есть доведение их до заданной степени точности.

Для отделения корней используются следующая теорема:

Теорема

Если непрерывная функция f(x) принимает значение разных знаков на концах отрезков [a, b], то есть 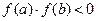, то внутри этого отрезка находится по крайней мере один корень уравнения f(x)=0. если производная 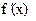сохраняет свой знак на отрезке [a, b], то корень будет единственный.