Обращение матрицы при разбиении на клетки

Разобьем матрицу А на четыре клетки

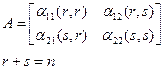
Будем искать обратную матрицу А^-1также в виде четырехклеточной матрицы:

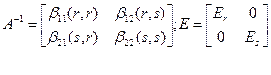
Так как 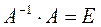, то перемножая эти матрицы, получим четыре уравнения:

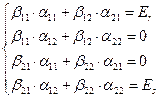(1)

E_s, E_r - единичные матрицы (rxr) (sxs)

Решая уравнения (1), получим:

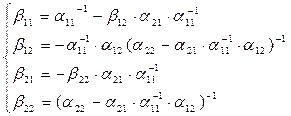
Вначале находим β₁₂ и β₂₂, а затем β₁₁ и β₂₁

В этом случае приходится обращать матрицы меньшей размерности:

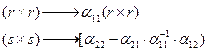
что дает существенный выигрыш в памяти ЭВМ.

4. Нахождение обратной матрицы методом Гаусса

Пусть дана неособенная матрица А и обратная – А^-1

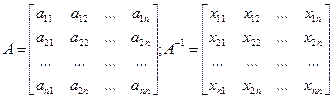
Для вычисления элементов обратной матрицы xij используем соотношение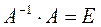

Умножая матрицы А и А^-1 и сравнивая каждый элемент произведения соответствующему элементу матрицы Е, получим систему уравнений с n² неизвестными x_ij(i,j (1,…n))

Умноженная почленно все строки матрицы А на первый столбец матрицы А^-1 получим первые n уравнений:

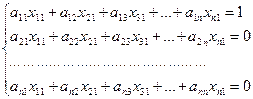(1)

Умножая почленно все строки матрицы А на второй столбец матрицы А^-1 получим вторые n уравнений:

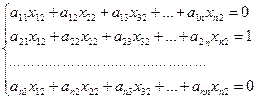(2)

И так далее.

В общем виде система n² уравнений 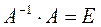может быть записана как

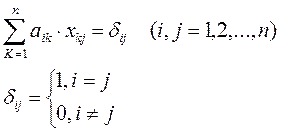
Все n уравнений (n систем вида (1), (2)) имеют одну и ту же матрицу А и различные свободные члены. Решаем систему методом Гаусса.

5. Применение метода итераций для умножения элементов обратной матрицы

Найдем обратную матрицу методом Гаусса.

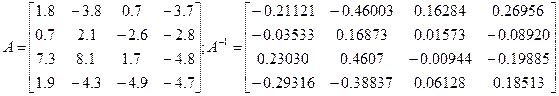
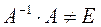из-за погрешностей вычислений.

Будем считать полученную матрицу 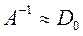- первым приближением к обратной матрице. Для уточнения элементов матрицы строим итерационный процесс (Демидович и Марон, и др.)

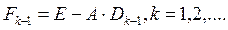(1)

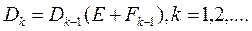(2)

Если 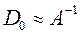, то итерационный процесс сходится.

Процесс (1), (2) продолжают до тех пор, пока элементы матрицы F по модулю не станут меньше заданного числа Е. Тогда полагают 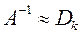(можно рассматривать какую-либо норму матрицы F)

Пример:

Уточнить элементы матрицы А^-1. Итерации продолжать до тех пор, пока элементы матрицы F_k по модулю не станут ≤5*10^-5

Решение:

1. Находим F₀ по формуле (1)

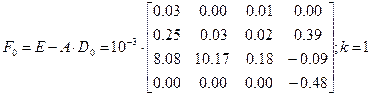
1. Находим D₀F₀

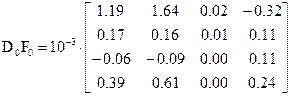
1. Находим

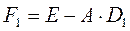
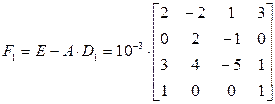
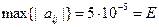
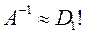
ЛЕКЦИЯ6