РАСЧЁТ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА

Расчёт доверительного интервала выполняется и в практических работах, и в домашней самостоятельной работе.

Для того чтобы рассчитать доверительный интервал для математического ожидания нормально распределённой случайной величины, необходимо проделать следующее:

1) задать доверительную вероятность P_дов. Причём часто берут вероятность, соответствующую симметричным интервалам нормального распределения по одной, двум и трём сигмам;

2) вычислить по выборочным данным выборочное среднее :

=

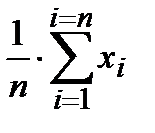
3) по тем же выборочным данным вычислить выборочное среднеквадратическое отклонение случайной величины

s =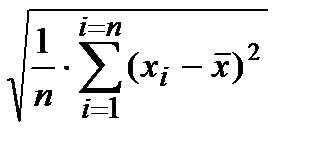

4) вычислить на основании выборочного среднеквадратического отклонения s оценку среднеквадратической ошибки оценки математического ожидания

=

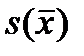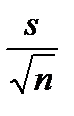
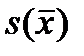5) отложить влево и вправо от среднеквадратическую ошибку столько раз, сколько сигм соответствует заданной доверительной вероятности (мы рассматривали симметричные интервал плюс-минус одна, две или три сигмы).

Для того, чтобы более наглядно представлять себе, что такое доверительный интервал и доверительная вероятность, нарисуем рисунок.

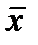
Доверительный интервал

Площадь под кривой = доверительная вероятность

Хвосты распределения

Выборочное среднее

Кривая нормального распределения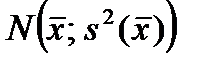

M(X)

По горизонтальной оси откладываем возможные значения неизвестного математического ожидания М(Х).

Отмечаем на горизонтальной оси вычисленное выборочное среднее.

Рисуем в обе стороны от выборочного среднего кривую нормального распределения шириной, соответствующей вычисленной оценке среднеквадратической ошибки оценки математического ожидания.

Границы доверительного интервала устанавливаем так, чтобы в его пределах оказались наибольшие значения кривой, т.е. те, которые наиболее близки к выборочному среднему значению.

А «хвосты», содержащие достаточно удалённые значения, при этом оказываются вне границ.

Площадь под кривой в пределах доверительного интервала – это доверительная вероятность.

Доверительные границы выбирают так, чтобы площади под «хвостами» были равны друг другу.

Применяются и другие, более удобные в использовании, значения доверительной вероятности, например:

0,90, 0,95, 0,99

(90%; 95%; 99%).

Им соответствуют симметричные доверительные интервалы

± 1,65× 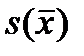, ± 1,96× 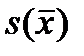, ± 2,58× ,

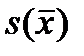Теперь такой вопрос:

Из чего надо исходить, чтобы задать доверительную вероятность?

Поскольку доверительная вероятность является мерой доверия к оценке, мы стремимся к тому, чтобы она была как можно ближе к единице. Кроме этого, очевидно, что более точной оценке соответствует более узкий доверительный интервал.

К сожалению, одновременно обеспечить и то, и другое невозможно. Почему?

Чем больше доверительная вероятность, тем меньше вероятность выхода оцениваемого математического ожидания за пределы доверительного интервала. Но для этого интервал приходится брать шире.

Если же мы сузим доверительный интервал, желая уменьшить неопределённость оценки, то этим самым мы увеличим вес «хвостов», а значит, уменьшим доверительную вероятность.

«Каждый охотник желает знать» доверительный интервал, в пределах которого с высокой вероятностью «сидит фазан». Экспедиции, разыскивающей затонувшее судно, нужно как можно точнее знать квадрат на море, где вероятнее всего обнаружить останки.

Единственный путь к получению узкого доверительного интервала при высокой доверительной вероятности – это увеличение объёма выборки.

Но сужение доверительного интервала происходит не быстро, а как 1/ 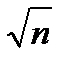. Т.е. при увеличении объёма выборки в 100 раз доверительный интервал сужается лишь в 10 раз.

Поэтому на практике просто задаются некоторым значением доверительной вероятности из указанного ряда «красивых» чисел.

Заключительное пояснение.

После проведения опытов и вычисления выборочного среднего возможность различных значений математического ожидания будет описываться кривой нормального распределения

.

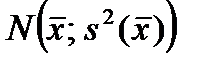Однако мы не можем говорить, что после проведения опытов математическое ожидание стало случайной величиной со средним и дисперсией .

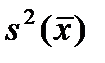Иными словами, кривая нормального распределения на рисунке не является кривой плотности распределения некоторой случайной величины.

Тогда что же это такое?