Необходимый объем выборки – это такое количество выборочных данных, которое обеспечивает выборочную среднеквадратическую ошибку оценки не хуже заданной.

Оцениваемая доля качественного признака находится в пределах от 0 до 1.

0 £ p £ 1.

Заданная ошибка оценки обычно выбирается из следующего ряда

s_зад = 0,10; 0,05; 0,01 (10%; 5%; 1%).

Помним, что доля – безразмерная величина. Поэтому и ошибка – тоже безразмерная величина.

Вспомним, как связаны выборочная среднеквадратическая ошибка оценки и объём выборки.

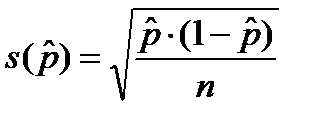
Из этой формулы можно выразить объем выборки

n = .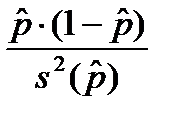

При равенстве ошибки заданному значению получается формула для необходимого объёма выборки

n_необх ³ .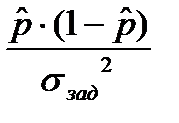

Знак «³» выбран потому, что объём выборки n_необх должен обеспечивать ошибку не хуже заданной s_зад.

Доля качественного признака в этой формуле 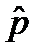оценивается по доступной выборке небольшого объема.

Округление в приведённом неравенстве при получении дробного числа необходимо производить в большую сторону, чтобы получить n_необх, обеспечивающий ошибку не хуже заданной s_зад.

Рассмотрим числовой пример. Центр изучения общественного мнения хочет оценить долю населения, поддерживающего главу администрации с ошибкой в 1%. Т.е. s_зад = 0,01.

Предположительно, хотя точно неизвестно, его поддерживает около половины населения. По доступной выборке небольшого объёма получилось такое значение доли

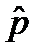= 0,4567 .

Подставляем эти данные в выражение.

n_необх ³ 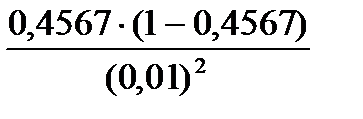= 0,248125 × 100² = 2481,25 » 2482 человека.

Округление объёма выборки сделано в большую сторону! Иначе ошибка увеличится и станет больше заданной.

Итог: необходимо опросить почти 2500 человек.

В результатах предвыборных опросов, которые приводят по телевидению, указывается примерно то же число опрошенных 1500-2000 человек.