ПОНЯТИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА
Этот вопрос важен тем, что он рассматривается в одной из практических работ, а также в самостоятельной работе.
Во многих случаях бывает удобно указывать не само значение оценки, а отрезок, интервал, содержащий неизвестное значение случайной величины или оцениваемой характеристики случайной величины.
Например, «среднее время ожидания троллейбуса от общежития 5–10 минут». Это не значит, что очередной троллейбус не может прийти через 1 или через 30 минут, но наиболее вероятное значение времени ожидания лежит в пределах от 5 до 10.
Для наглядности рассмотрим пример: стрельбу по мишени из винтовки.
Винтовка пристрелянная, у стрелка зрение хорошее, рука твёрдая.
Но из-за дыхания, ударов сердца, дрожания рук точного попадания, как правило, нет.
Подойдём к опыту со стрельбой с двух сторон: до выстрела и после выстрела.
1. Вешается новая мишень. До выстрела можно сказать, что отверстие от пули будет находиться где-то вблизи от центра мишени.
2. Выстрел по мишени сделан, после чего мишень убрана. В стене осталось отверстие от пули. Не зная, где была прикреплена мишень, можно сказать, что её центр находился где-то вблизи от пулевого отверстия в стене.
Взаимное удалённость пулевого отверстия и центра мишени в обоих случаях определяется только точностью стрельбы.
Теперь переформулируем наши наблюдения (при этом первое будет относиться к теории вероятности, второе – к статистике).
Если известно значение математического ожидания, то весьма вероятно, что в результате опыта случайная величина примет значение, мало отличающееся от математического ожидания.
Если математическое ожидание неизвестно, а на основании опыта получено значение случайной величины, то весьма вероятно, что математическое ожидание имеет значение, мало отличающееся от полученного в опыте значения.
Что значит «мало отличающееся»? Отличие значения случайной величины в опыте и математического ожидания соизмеримо со среднеквадратическим отклонением s.
Сделаем рисунок к первому выводу.
| M(X) |
| M(X) – s |
| M(X) + s |
| интервал допуска |
| x |
Вдоль горизонтальной оси отложены возможные значения случайной величины. Отметим на ней значение математического ожидания. Влево и вправо отложим отрезки величиной в среднеквадратическое отклонение. Вблизи полученного отрезка нарисуем сравнимый с ним по размерам интервал, который может быть назван интервалом допуска. Обоснованно ожидать, что значения случайной величины будут часто оказываться внутри него.
Для второго вывода можно также нарисовать картинку.
| M(X) |
| x – s |
| x + s |
| доверительный интервал |
| x |
По горизонтальной оси будем откладывать значения неизвестного оцениваемого математического ожидания.
На этой же оси отметим точку, соответствующую значению случайной величины, полученной в опыте. Отложим также влево и вправо по одному среднеквадратическому отклонению. Вблизи полученного отрезка также нарисуем интервал, сравнимый с отрезком по размеру. Этот интервал называется доверительным интервалом. Неизвестное математическое ожидание, вероятнее всего, находится внутри этого интервала.
Для примера со стрельбой по мишени s определяется кучностью стрельбы используемой винтовки.
Нам доверительный интервал нужен для оценивания математического ожидания. При этом случайной величиной у нас является выборочное среднее, а неизвестной искомой величиной – математическое ожидание.
Определение.
Доверительный интервал – это отрезок на оси значений оцениваемой характеристики случайной величины(например, математического ожидания), который с заданной вероятностью накрывает неизвестное значение оцениваемой характеристики.(Накрывает или, другими словами, содержит внутри себя.)
В нашем примере доверительный интервал располагается в окрестности значения выборочного среднего и содержит внутри себя неизвестное оцениваемое математическое ожидание с весьма высокой вероятностью.
Вероятность того, что оцениваемое математическое ожидание окажется в пределах доверительного интервала называется доверительной вероятностью.
Доверительная вероятность задаётся. Она является мерой доверия к оценке.
Точки на оси, ограничивающие доверительный интервал, называются доверительными границами.
Границы доверительного интервала однозначно связаны с доверительной вероятностью.
Выясним, какова эта связь для нормально распределённой случайной величины.
Рассматривая симметричные интервалы нормального распределения, мы записывали вероятность попадания значения случайной величины Х в интервал ±s
P( M(X) – s £ Х < M(X) + s ) = 0,682 .
Почему мы рассматриваем именно нормально распределённую случайную величину?
Математиками установлено, что при объёме выборки большем 25 любая статистика имеет распределение очень близкое к нормальному. И выборочное среднее  здесь не исключение.
здесь не исключение.
Математическое ожидание этого распределения выборочного среднего 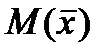 совпадает с математическим ожиданием случайной величины M(X), а дисперсия равна
совпадает с математическим ожиданием случайной величины M(X), а дисперсия равна 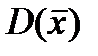 или, при другом обозначении,
или, при другом обозначении, 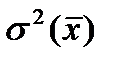 .
.
Поэтому для выборочного среднего  , вычисленного по выборке объёмом n, справедливо то же соотношение
, вычисленного по выборке объёмом n, справедливо то же соотношение
P( M(X) – 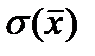 £
£  < M(X) +
< M(X) + 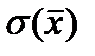 ) = 0,682 .
) = 0,682 .
Т.е. 0,682 – это вероятность того, что выборочное среднее  окажется внутри интервала допуска шириной ±
окажется внутри интервала допуска шириной ± 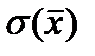 .
.
Путём нескольких несложных математических преобразований из предыдущего равенства можно строго получить похожее выражение для математического ожидания.
Для этого мы преобразуем неравенство, стоящее в скобках, но так, чтобы его вероятность осталась прежней.
Вычтем из всех трёх частей внутреннего двойного неравенства математическое ожидание. При этом справедливость неравенства не нарушится, а его вероятность не изменится.
– M(X): P( – 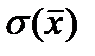 £
£  – M(X) <
– M(X) < 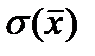 ) = 0,682 .
) = 0,682 .
Теперь из всех частей неравенства вычтем выборочное среднее.
–  : P( –
: P( –  –
– 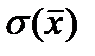 £ – M(X) < –
£ – M(X) < –  +
+ 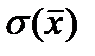 ) = 0,682 .
) = 0,682 .
И, наконец, умножим все части неравенства на «–1». При этом знаки неравенства изменятся на противоположные.
× (-1): P(  +
+ 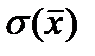 ³ M(X) >
³ M(X) >  –
– 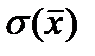 ) = 0,682 .
) = 0,682 .
Перепишем полученное выражение, чтобы неравенство шло в порядке возрастания
P(  –
– 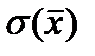 < M(X) £
< M(X) £  +
+ 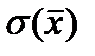 ) = 0,682 .
) = 0,682 .
Ввиду того, что точное значение 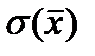 не известно, заменяем его его оценкой
не известно, заменяем его его оценкой 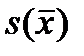 :
:
P(  –
– 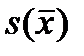 < M(X) £
< M(X) £  +
+ 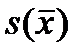 ) ≈ 0,682 .
) ≈ 0,682 .
Равенство при этом перестаёт быть точным, но мы в дальнейшем будем на это закрывать глаза.
Смысл полученной записи следующий:
неизвестное математическое ожидание M(X) находится в границах ± 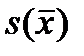 вокруг значения выборочного среднего
вокруг значения выборочного среднего  с вероятностью 0,682.
с вероятностью 0,682.
Таким образом, 0,682 – это доверительная вероятность.
А границы ± 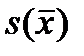 от
от  задают доверительный интервал, накрывающий неизвестное оцениваемое значение математического ожидания M(X).
задают доверительный интервал, накрывающий неизвестное оцениваемое значение математического ожидания M(X).
Теперь у нас имеется связь между доверительной вероятностью и границами доверительного интервала. При условии, конечно, что наша случайная величина имеет нормальное распределение.
Если мы вдвое увеличим интервал и сделаем его от  – 2 ×
– 2 × 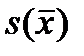 до
до  + 2 ×
+ 2 × 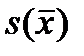 ,
,
т.е. шириной по две среднеквадратические ошибки в каждую сторону, то ему будет соответствовать бòльшая доверительная вероятность: Pдов = 0,955.
Если интервал будет от  – 3 ×
– 3 × 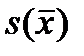 до
до  + 3 ×
+ 3 × 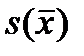 ,
,
т.е. по три среднеквадратические ошибки, то доверительная вероятность ещё больше увеличится: Pдов = 0,997.
Дата добавления: 2021-01-26; просмотров: 604;











