ВЫБОРОЧНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ

Выборочный коэффициент корреляции – это оценка неизвестного значения коэффициента корреляции наблюдаемых в опыте случайных величин X и Y по парам выборочных данных (x₁, y₁), (x₂, y₂), …, (x_n, y_n).

Общепринятое буквенное обозначение – r .

Область возможных значений выборочного коэффициента корреляции также от –1 до 1.

Выборочный коэффициент корреляции численно показывает тесноту линейной статистической связи между отклонениями выборочных значений двух наблюдаемых в опыте случайных величин X и Y от своих выборочных средних и .

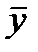Формула для вычисления коэффициента корреляции по выборке такова:

r = =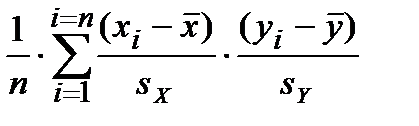

(среднее арифметическое произведений относительных отклонений в каждой выборочной паре значений двух случайных величин)

= .

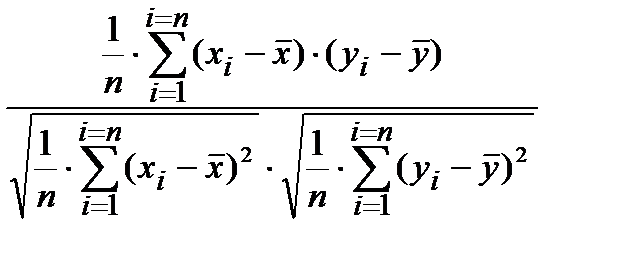Поскольку выборочные значения случайны, выборочный коэффициент корреляции – это случайная величина.

Рисунки к выборочному коэффициенту корреляции – это точечные диаграммы. Одну из них мы рисовали. Для роста и веса.

Точечные диаграммы при различных значениях коэффициента корреляции будут нами строиться на Excel в практической работе на ЭВМ.

Механизм действия приведённой формулы прост.

В числителе – сумма произведений отклонений. Знаменатель всегда положительный.

Следовательно, знак результата будет определяться числителем.

Предположим коэффициент корреляции случайных величин X и Y больше нуля

r > 0.

Это значит, что наиболее вероятны такие пары значений случайных величин, в которых случайные величины отклоняются от своих средних либо одновременно в большую, либо одновременно в меньшую сторону.

При r > 0 , если (x_i – 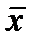) > 0, то вероятнее всего, что и

(y_i – 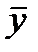) > 0.

Произведение двух положительных отклонений будет положительным

(x_i – 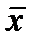) · (y_i – 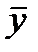) > 0.

А если (x_i – 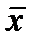) < 0, то вероятнее всего, что и (y_i – 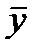) < 0.

Но произведение отклонений по-прежнему будет положительным

(x_i – 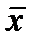) · (y_i – 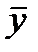) > 0.

Таким образом, в числителе будет накапливаться сумма, состоящая преимущественно из положительных чисел, и в итоге получится положительное значение, как и r.

Если же r < 0, то при (x_i – 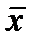) > 0 вероятнее всего, что

(y_i – 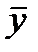) < 0

В итоге (x_i – 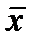) · (y_i – 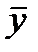) < 0.

При (x_i – 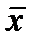) < 0 вероятнее всего, что (y_i – 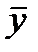) > 0

Но по-прежнему (x_i – 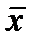) · (y_i – 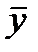) < 0.

В числителе будет накапливаться отрицательная величина, как и r .