НЕОБХОДИМЫЙ ОБЪЕМ ВЫБОРКИ ПРИ ОЦЕНКЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ КОЛИЧЕСТВЕННОГО ПРИЗНАКА

Есть такой вопрос в самостоятельной работе.

Мы выяснили, что для определения необходимого объема выборки требуется задать предельно допустимую среднеквадратическую ошибку.

При оценке качественного признака ошибка была долей. А в случае количественного признака ошибка будет выражаться в тех же единицах измерения, что и сам количественный признак, например: в рублях, в килограммах.

Для того чтобы ошибка также была долей и могла выражаться в процентах, надо вычислять относительную ошибку.

Относительная ошибкачисленно равна отношению выборочной среднеквадратической ошибки оценки к значению оценки:

d = .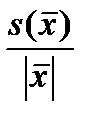

Здесь d – маленькая греческая буква дельта. Модуль – для положительности итогового значения.

Другое название относительной ошибки – относительная погрешность. Из названия всё понятно.

Заданная относительная ошибка оценки обычно выбирается из следующего ряда:

d_зад = 0,10 , 0,05 , 0,01 (10 %, 5 %, 1 %).

Приступаем к получению выражения для необходимого объёма выборки.

Мы знаем, как связаны объём выборки и выборочная среднеквадратическая ошибка:

= .

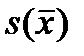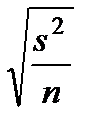Выражаем отсюда объём выборки

n = =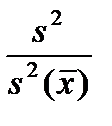

и, пользуясь выражением для d, заменяем оценку ошибки

= .

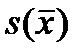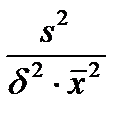Если в знаменателе в качестве d подставить заданную относительную ошибку d_зад, то получим выражение для необходимого объема выборки

n_необх ³ .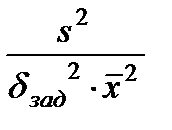

Выборочная дисперсия s² и оценка среднего определяются по доступной выборке небольшого объема. Округление выполняется в большую сторону.