Оценка доверительного интервала уравнения регрессии.

Так как величины xi и yi, на основе которых выводится уравнение регрессии, являются величинами случайными, уравнение регрессии должно быть записано в форме: y=f(x)±Δ, где Δ – полуширина доверительного интервала. Δ=f(x), так как при каждом фиксированном x будет своё значение σ_y. Простейшая оценка полуширины доверительного интервала уравнения регрессии определяется с помощью гарантийного коэффициента Стьюдента.

Δ=±t_стσ_xy; σ_xy – среднеквадратическое отклонение значений y относительно прямой регрессии.

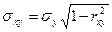
Этот способ является простейшим и не учитывает изменения ширины доверительного интервала вдоль линии регрессии.

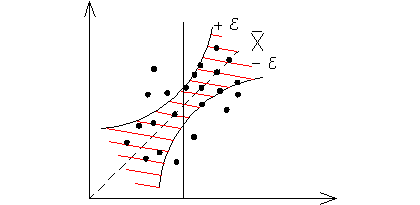
В уравнении регрессии y=a+bx a и b являются величинами случайными и могут быть записаны:

;

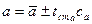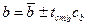
где c_a и c_b – дисперсии коэффициентов a и b.

В этом случае влияние доверительных интервалов будет разным.

Если изменяется ±t_стc_a:

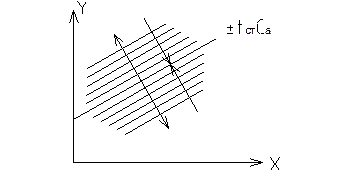
Если изменяется ±t_стc_b:

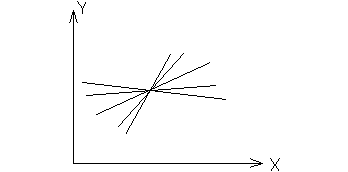
В итоге мы получаем:

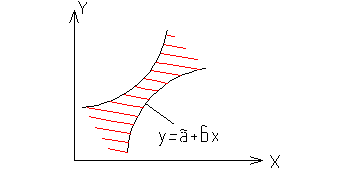
Таким образом, уравнение регрессии представляет собой не линию, а полосу, в которой с заданной доверительной вероятностью P_дов находится истинное положение линии y=a+bx.

Кроме этого, при построении доверительного интервала возникает вопрос о том, насколько достоверны значения коэффициентов a и b – значимость коэффициентов уравнения регрессии, то есть, величины a и b, полученные случайным образом, могут иметь низкую достоверность и их конкретная величина статистически не значима. Значимость коэффициентов оценивается с помощью гарантийных коэффициентов Стьюдента, аналогичным образом, который был показан выше при очистке ряда измерений, то есть, вычисляется расчётное значение коэффициента Стьюдента отдельно для a и b и сравнивается с табличным значением. Если t_ст^расч>t_ст^табл, то соответствующий коэффициент не значим, и, соответственно, не значим другой.