Метод дробных реплик

Во многих сложных физических процессах число фактором может достигать количества 5-7, опытов – 25-49. Кроме этого, каждое значение факторов для проверки и установления статистической устойчивости может потребовать от 3 до 7 опытов. Число опытов для планов типа 2ⁿ можно уменьшить почти в 2 раза, используя половину матрицы. Геометрически это объяснимо тем, что, например, план-куб будет полностью определён, если зафиксировать его диагональную плоскость.

В этом случае основу матрицы планирования составляет план двухфакторного эксперимента:

Варьирование третьего фактора соответствует произведению .

Такой способ при выполнении следующего условия.

В уравнении регрессии a₀=x₀. В этом случае получим следующую матрицу планирования:

№ опыта
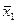
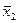
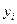
	+1	+1	+1	+1	y1
	+1	+1	-1	-1	y2
	+1	-1	+1	-1	y3
	+1	-1	-1	+1	y4

y=a₀+a₁x₁+a₂x₂+a₁₂x₁x₂

x₁x₂=x₃

Коэффициенты уравнения регрессии вычисляются по формуле:

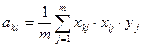
Существует возможность применения планов эксперимента, когда некоторые факторы приравнивают к произведению нескольких выбранных факторов.

y=a₀+a₁x₁+a₂x₂+ a₃x₃+ a₄x₄+ a₅x₅+ a₆x₆+ a₇x₇

При планировании со смешиванием применяют планы типа 2^n-p, где n – число факторов, p – число факторов, заменяемых произведениями. Например, план 2^7-4: ; ; ;

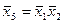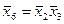Таким образом, можно значительно уменьшить количество опытов, однако применение этого способа сопряжено с рядом условий, одно из которых состоит в том, что вид поверхности отклика точно является плоскостью в n-мерном пространстве.

14. Метод центрального композитного планирования

Этот метод применим в том случае, если функция отклика описывается поверхностью второго порядка. Например, такой:

y=a₀+a₁x₁+a₁x₂+a₁₂x₁x₂+a₁₁x₁²+a₂₂x₂²

В этом случае план линейного полинома дополняется опытами в промежутках (звёздных).

Количество опытов определяется так: m=2ⁿ+2n+1

Графический план выглядит так:

Матрица планирования дополняется по сравнению с линейной моделью.

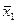
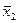
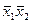
	№				y
Полиофактический эксперимент для линейной модели		+1	-1	-1
	+1	+1	+1
	+1	-1	-1
	+1	+1	+1
Центральная звёздная точка
			+1
		-1
			+1
		-1

Для планов ЦКП существуют простые формулы для определения коэффициентов уравнения регрессии. Для каждого из видов ЦКП существуют специальные таблицы, а сами ЦКП входят в состав всех математических пакетов (раздел «Статика», подраздел «Планирование эксперимента»). В этом программном обеспечении производятся оценки дисперсии коэффициентов, проверяется их значимость и адекватность уравнению регрессии по критерию Фишера. Более подробны сведения о планировании эксперимента находятся в книгах:

Михайлов В. И., Федосов К. М. «Планирование эксперимента в судостроении», Л, Судостроение, 1978 – 159 с.

Шенк Х. «Теория инженерного эксперимента» - М, Мир, 1972 – 381 стр.

15. Рандомизация планов экспериментов

Для того, чтобы неучтённые внешние условия и их изменения в процессе проведения экспериментов накладывались на результаты опытов равномерно, последовательность опытов чередуют случайным образом – рандомизация. Для этого используют таблицу случайных чисел с равномерным распределением. Последовательность действий:

№							№
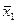
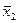
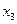
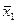
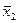
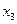
	+1	-1	+1					+1	+1	+1
	-1	-1	+1
	+1	+1	+1
	-1	+1	+1
	+1	-1	-1
	-1	-1	-1
	+1	+1	-1
	-1	+1	-1

Рандомизация имеет большое значение для серий опытов при проверке воспроизводимости и адекватности. Особенно важна рандомизация в однофакторном эксперименте, когда велика вероятность ошибки, которая называется «ожидание результата». Тем не менее, во многих физических процессах конечный результат зависит от предыстории процесса и рандомизация не позволит учесть это обстоятельство. Поэтому исследованию всякого мало изученного процесса должны предшествовать предварительные опыты для выявления качественной картины происходящего явления.