Проверка адекватности теоретических зависимостей экспериментом
Если теоретические и экспериментальные зависимости описываются линейными уравнениями y=f(x), то проверка адекватности теоретических результатов производится следующим образом:
1) Проводится эксперимент, по результатам которого строится уравнение регрессии с соответствующим интервалом доверительных значений.
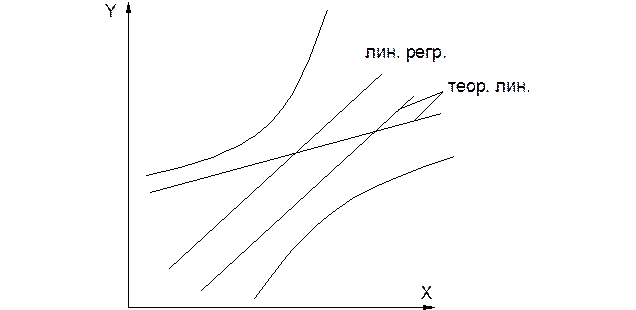
2) Производится численный расчёт функций y=f(x) по теоретической зависимости и наносится на график. Если теоретическая линия лежит внутри полосы доверительных значений, то делается вывод, что результаты эксперимента подтверждают достоверность теории, теоретическая линия является адекватной. Это справедливо при условии, что a и b значимы, rxy≠0 с доверительной вероятностью Pдов.
В том случае, когда теоретическая зависимость описывается функцией нескольких переменных y=f(x1; x2; x3;…), регрессия является множественной и нелинейной, например:
y=a0+b1x1+b2x2+b3x3…+bnx1x2+bn+1x1x3…
В этом случае доверительной является не полоса, а некоторая четырёхмерная область, которая не представляется графически. В этом случае задача формально решается с помощью теории Стьюдента, которую для множественной регрессии переработал Фишер. Критерий Фишера: при многомерной нелинейное регрессии необходимо прежде всего доказать воспроизводимость результатов опытов. Для этого выполняется m серий опытов по n опытов в каждой серии.
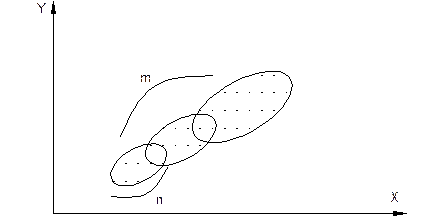
Опыты будут считаться воспроизводимыми, если результаты в каждой сериипринадлежат к одной и той же статистической зависимости. Последовательность проверки воспроизводимости по критерию Кохрена:
1) Проводим несколько серий опытов (m>4) по несколько (n>5) опытов в каждой серии.
2) Для каждой серии определяем дисперсию Di.
3) Определяем расчётный критерий Кохрена:
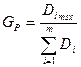
4) По таблице находим теоретическое значение критерия Gтеор. Если Gр>Gтеор, опыты не воспроизводимы.
Если опыты воспроизводимы, то проводится проверка адекватности теоретического результата данным опытом.
После проведения опытов рассчитывается критерий Фишера:
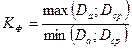
где Da – дисперсия адекватности, своя для каждой серии опытов.
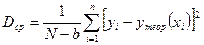 ;
; 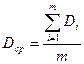
b – число коэффициентов в уравнении регрессии.
D – средняя дисперсия по числу серий.
Полученное значение KФ сравнивается с теоретическим значением. Если KФ<KФтеор, то уравнение регрессии адекватно теоретической зависимости.
11. Основные принципы рационального планирования эксперимента
Эксперименты в судостроении отличаются затратами средств, поэтому без предварительного планирования можно получить лишний материал и не получить необходимого, поэтому, прежде чем приступать к эксперименту, надо разработать проект. Самый общий проект называется методология.
Для многих видов эксперимента методология разработана и изложена в руководящих документах, учебниках, инструкциях. Например, проведение буксировочных испытаний в бассейне, измерение индикаторной мощности механизмов, испытание прочности узлов конструкции и т. п. Методология содержит и определяет следующие составные части:
1) План программы эксперимента.
2) Разработка проекта и создание экспериментальной установки.
3) Математическое планирование эксперимента.
4) Проведение экспериментов.
5) Обработка и анализ результатов.
При использовании современных средств регистрации и обработки пункты 4 и 5 выполняются одновременно.
Разработка плана программы эксперимента
Включает в себя:
1) Рабочую гипотезу с выбором основных и второстепенных факторов.
2) Цель эксперимента.
3) Выбор варьируемых факторов.
4) Проект (технология) проведения эксперимента.
Если эксперименты проводятся с объектами, для которых разработаны методологии, то в начале производятся настроечные опыты для оценки характера явлений и выработки рабочей гипотезы.
С помощью методов математического планирования и предварительных опытов определяется минимально необходимое количество измерений, которое должно обеспечивать устойчивое среднее значение измеряемой величины.
План-программа проведения эксперимента
По своей сути этот документ является подробной технологией выполнения экспериментальных работ. Составляется в виде таблицы.
| Укрупнённые операции | Детализация | Кол. исп. | Средства обеспечения | Время |
| 8. Зачистка ледового бассейна | 8.1 Подключение шланга для слива воды | Шланг | 0,2 ч | |
| 8.2 Промывка сливной трубы от льда | - | 0,5 ч | ||
| 8.3 Слив воды | - | 5 ч | ||
| 8.4 Отрубка и уборка льда | Лом, ледорубы, лопаты | 2 ч |
Разработка формы протокола
Протокол опыта – таблица, в которой приведены все необходимые данные для возможности повторения данного опыта, а также полученные результаты. Каждый протокол должен содержать фамилии и подписи участников эксперимента.
12. Основы математического планирования эксперимента. Варианты экспериментального исследования.
I y=5l-2x
Для проверки адекватности этой зависимости количество опытов минимально. Оно является статистическими ошибками при измерении y и задании x. Минимальное количество – три опыта.
II y=al-6x
Теоретически получена зависимость, где a и b – неизвестные эмпирические коэффициенты. При малом разбросе результатов измерения достаточно шести опытов (три на каждый коэффициент).
III Теоретической зависимости нет, а результат задаётся нелинейной формы.
y=a+b1x1+b2x2+b3x1x2…+bnx12
В этом случае для определения неизвестных коэффициентов необходимо проводить большое количество опытов, если не применяются методы математического планирования.
Принципы математического планирования экспериментов
Этот метод определяет условия оптимального проведения эксперимента даже при неполном знании физической сути явления. Существует два вида планов:
I Классический y=f(x1; x2; x3; x4)
При этом для выявления полной формы функции необходимо проведение пяти экспериментов по каждому фактору x. При четырёх факторах в этом плане требуется 625 экспериментов.
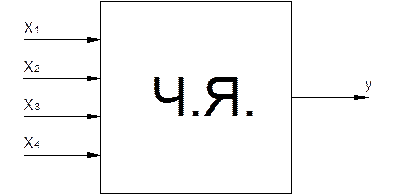
II Полнофакторный эксперимент, в котором в самом благоприятном случае 25 опытов. Метод полного факторного эксперимента заключается в следующем: функция отклика раскладывается в ряд Тейлора.
y=β0+β1x1-…βixi+βnxn+…βiixixj+βijxixj+…+ε
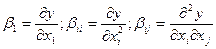
Это выражение эквивалентно уравнению регрессии, в котором коэффициенты могут быть определены методом наименьших квадратов:
y=a0+a1x1+…aiixii…+aixi2
Из-за трудностей анализа получаемых результатов многие прикладные методы и программы используют зависимость не выше квадратичной. Например, для двух факторов:
y=a0+a1x1+a2x+a3x1x2+...+a4x12+a5x22 (*)
Для нахождения коэффициента aj (j=0, 1…k) по методу наименьших квадратов требуется k+1 опытов.
Уравнение (*) считается справедливым в некоторой области Ω, называемой областью планирования эксперимента. x1, x2, …, xnЄΩ называется планом эксперимента, который может быть записан в виде матрицы.
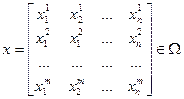
Количество строк в матрице n выбирается из возможности проведения проверок на значимость, адекватность, воспроизводимость m≥k+1.
Значения x и y в начале являются конкретными факторами в опыте. Для удобства составления матрицы планирования значения факторов xik нормируют так, чтобы -1<xik<+1. Нормирование производится по формуле:
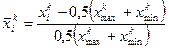
Уравнение регрессии является функцией отклика. Это уравнение некоторой поверхности. Для правильного планирования эксперимента необходимо заранее знать поверхность функции отклика.
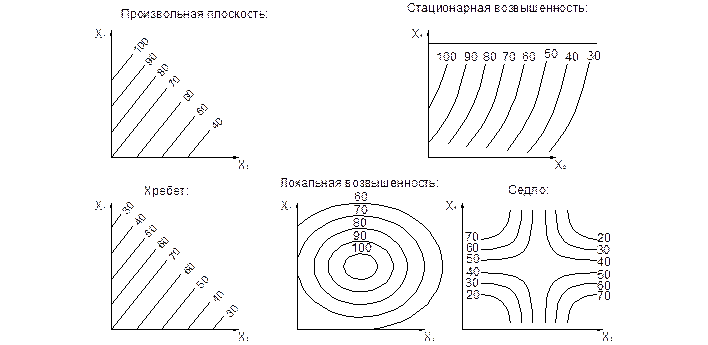
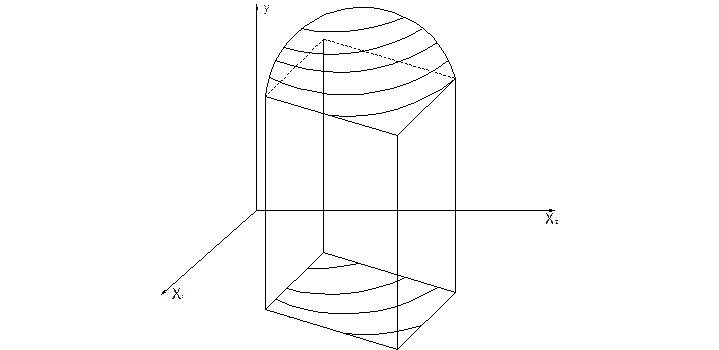
Для каждого из видов в справочниках можно найти математическое выражение, которое и можно принять в качестве формы уравнения регрессии. В простейшем случае, если функция отклика представляет собой плоскость, уравнение регрессии имеет вид:
y=a0+a1x1+a2x2
Для того, чтобы определить коэффициенты уравнения регрессии, нужно провести k+1 опыт, рационально выбрать значения факторов 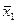 и
и 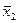 (чёрточка – нормированные значения) на границе области планирования. Количество значений фактора в плане называется уровнем варьирования. В данном случае два уровня (+1; -1)
(чёрточка – нормированные значения) на границе области планирования. Количество значений фактора в плане называется уровнем варьирования. В данном случае два уровня (+1; -1)
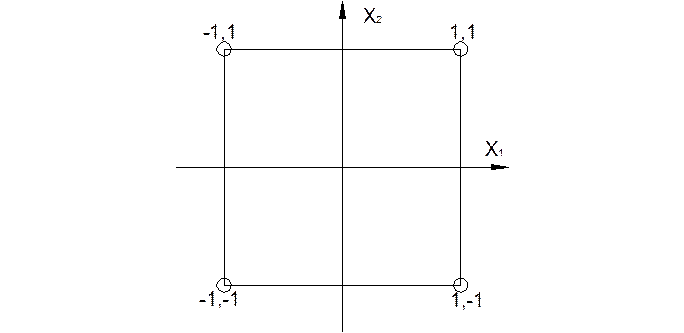
Этот план в форме матрицы выглядит следующим образом:
| № опыта | x1 | x2 | y |
| -1 | -1 | ||
| -1 | |||
| -1 |
Общий принцип построения планов для линейного полинома носит название «План 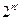 », где n – число факторов. Общее число опытов Nопытов=2n
», где n – число факторов. Общее число опытов Nопытов=2n
y=a0-a1x1+a2x2+a3x3
Если плоскость записывается в пятимерном пространстве, число опытов для определения коэффициентов составит 8.
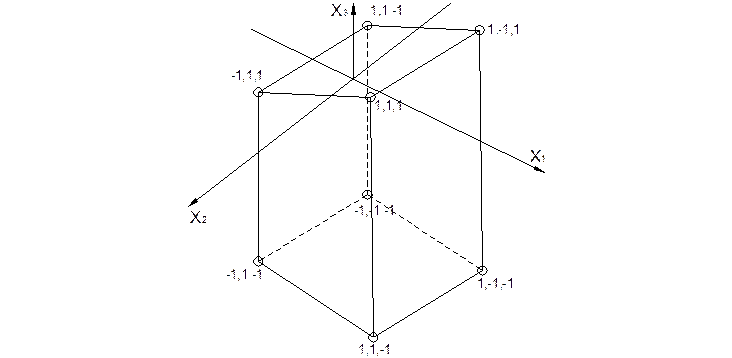
| № опыта | x1 | x2 | x3 | y |
| -1 | -1 | |||
| -1 | ||||
| -1 | ||||
| -1 | -1 | -1 | ||
| -1 | -1 | |||
| -1 | -1 | |||
| -1 |
Матрица планирования обладает следующими свойствами:
1) 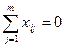 ; 2)
; 2) 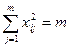 ; 3)
; 3) 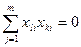 , если l≠k
, если l≠k
Где i, l, k – номера факторов.
Коэффициенты линейного уравнения регрессии определяются очень простым способом.
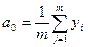 ;
; 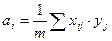
Некоторые из коэффициентов регрессии могут оказаться незначимыми. Коэффициент регрессии значим и им нельзя пренебрегать, если |a|>Da·tст, где tст – гарантийный коэффициент Стьюдента, Da – дисперсия коэффициента a.
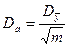
Кроме этого, необходимо доказать: являются воспроизводимыми с помощью критерия Фишера.
Дата добавления: 2021-01-26; просмотров: 543;











