Применение ЭВМ в научных исследованиях

Существует много путей и направлений такого применения. Один из самых первых – применение ЭВМ для решения задач численными методами. Численный метод, в отличие от аналитического, предполагает доведение решения задачи до решения системы уравнений, поиска экстремума в поле генерируемых данных. Второе направление использования ЭВМ – регистрация и обработка экспериментальных данных. Для этого применяется АЦП. Третье направление – использование пакетов для расчёта параметров деформации, перемещения, энергетических характеристик сплошных и дискретных объектов. Эти пакеты основаны на использовании метода конечных элементов. При использовании таких пакетов исследуемый объект разбивается на ряд небольших конечных элементов, внутри которых изменения параметров происходят по линейным законам. Используя условия равновесия, непрерывности, сохранения энергии, составляются уравнения, связывающие состояние элемента с координатами или кинематическими параметрами в узлах. После этого с помощью основных физических принципов (минимума потенциальной энергии, равенства кинетической и потенциальной энергий и др.) полученные уравнения с бесконечным числом неизвестных приводятся к уравнениям, в которых число уравнения равно числу неизвестных. После решения системы этих уравнений получают значения параметров объекта в узловых точках конечных элементов. Для большинства инженерных задач такие пакеты разработаны и используются в проектных и исследовательских работах.

Главная задача исследователя состоит в правильном выборе размеров и формы конечных элементов объекта и правильной обработки полученных результатов. Несмотря на автоматизированность выполнения основных операций по решению задачи исследователь должен понимать суть используемого метода в его предельной возможности и ограничениях. По своей сути численные методы решения сложных задач с объектами, разбиваемыми на конечные элементы, представляют собой вычислительный эксперимент, для которого, как для теоретического метода, требуется проверка адекватности. Такая проверка может быть осуществлена путём сравнения полученных результатов с экспериментальными данными или данными, полученными аналитическим методом (так называемыми точными решениями).

Проблемы применения численных методов

1) Сходимость. Когда сплошная расчётная область рассматривается как совокупность элементов конечной длины, возникает погрешность, обусловленная несовпадением реальной картины деформирования сплошной среды и её конечной элементной моделью.

Например, «точная» математическая модель даёт точное теоретическое решение для пластинки на упругом основании, когда основные законы её деформирования выражены через бесконечно малые размеры элементов. При составлении численной модели бесконечно малые элементы заменяются конечными с потерей точности. (б) Чем мельче будет разбиение расчётной области на конечные элементы, тем ближе численное решение к точному теоретическому. Поэтому при использовании любого численного метода необходима оценка погрешности этого метода. Кроме этого, может возникать ситуация, когда численная модель принципиально не соответствует физической модели. Для того, чтобы оценить эту погрешность, необходимо с помощью данного численного метода выполнить следующее:

1. Найти известное теоретическое решение из класса подобных задач и показать, что численное решение обладает сходимостью к «точному» теоретическому.

2. Альтернатива. Следует провести эксперимент с объектом данного класса и сравнить экспериментальные значения с численными.

2) Устойчивость численного решения. При измельчении расчётной области в начале, как правило, результат приближается к точному.

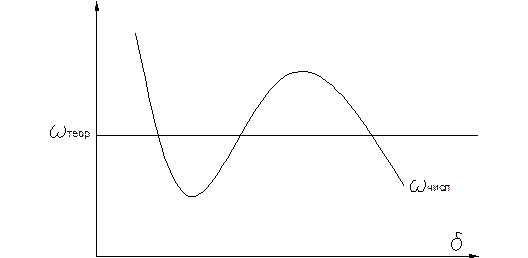
Однако существует предел измельчения элементов, начиная с которого результат расчёта отклоняется от точного и начинает расходиться всё больше. Как правило, это связано с конечностью представления чисел процесса. В большинстве пакетов используется точность 16 чисел Мантисса (после запятой).

Поэтому на аналогичной простейшей модели, где имеется точное решение, должна производиться также проверка устойчивости. На основании этих двух проверок обосновывается применение численного метода.