Подбор эмпирических формул
Имеется табличная функция yi=f(xi)
Требуется подобрать алгебраическое выражение:
y=axn+bxn-1…+c
x=xi; y=yi
Эта задача носит общий математический характер и называется задачей аппроксимации. Аппроксимация требуется в следующих случаях:
1) Когда математическая зависимость есть, но пользоваться ей крайне трудно из-за сложной структуры формул. Например, формулы Эйлера и т. д.
2) Когда данные получены экспериментально, а математическая модель явления неизвестна, создаётся эмпирическая формула. Требования к формуле:
Если имеется экспериментальная зависимость, её можно аппроксимировать.
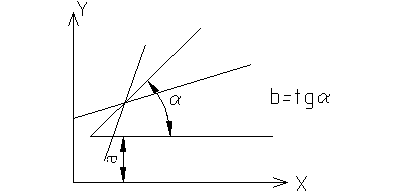
Для объективной оценки используют метод объективных квадратов. Его суть в том, что линия проводится так, чтобы сумма квадратичных отклонений точек от прямой была минимальной. Отклонение определяется так: 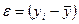 ,
, 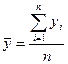 , где yi – экспериментальная точка,
, где yi – экспериментальная точка, 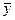 - значение функции на прямой.
- значение функции на прямой.
Таким образом, нужно подобрать такие значения a и b, чтобы 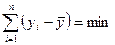
Так как 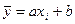 , то
, то 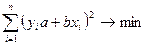
Условия экстремума имеют вид:
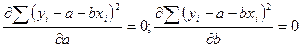
В результате дифференцирования получается система двух уравнений:
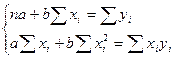
Из которых определяется:
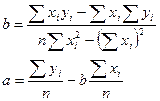
Этот способ применим для любой сложной кривой, описываемой полиномом:
y=a1xn+a2xn-1+a3xn-2…
Однако для практических инженерных приложений, как правило, используют простые линейные зависимости, к которым можно приводить зависимости нелинейные путём линеаризации. Линеаризация состоит в замене переменных в аппроксимирующей функции (линейная). Очень большую роль играет выбор аппроксимирующей функции. Рекомендации: если функция имеет вид y=axb.
lny=a+b∙lnx
Y=lny; X=lnx; Y=a+bX
Таким образом, для построения этой зависимости надо прологарифмировать значения xi и yi
y=a∙lbx
lny=a+bx; Y=a+bx
y=a+b/x; y=a+bX; X=1/x
Многие графики разных по структуре функций имеют одинаковый вид. Методом наименьших квадратов нельзя определить, какая из аппроксимирующих функций наилучшим образом аппроксимирует экспериментальные значения. Эти вопросы могут быть решены методами регрессионно-корелляционного анализа.
Случайные величины, измеряемые в опытах, или же полученные в результате обработки данных наблюдений (данные по различным судам) могут быть:
а) Независимыми.
б) Связанными статистической зависимостью.
Статистическая зависимость отличается от функциональной тем, что в ней изменение одной величины влияет на параметры распределения другой величины.
Если в результате изменения одной величины изменяется математическое ожидание (среднее Vср) другой величины, такая статистическая зависимость называется корелляционной, то есть, если между x и y существует корелляционная связь, то при изменении  .
.
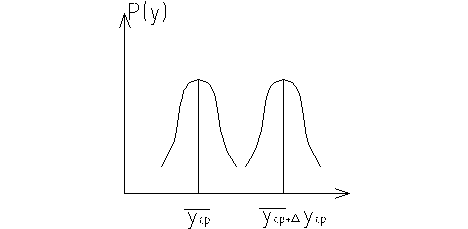
Таким образом, между двумя случайными величинами существует корелляционная зависимость, если каждое значение одной из них соответствует множеству значений другой, но её среднее значение зависит от первой величины, например, рост и вес человека.
Существует два частных предельных случая корелляции:
а) Полное отсутствие; б) Однозначная функциональная зависимость (y=f(x)).
Корелляция бывает парная, множественная, а также линейная. Далее мы будем рассматривать только парную линейную корелляцию.
Главная задача корелляционного анализа: определить степень близости статистической зависимости к функциональной. Субъективную оценку можно сделать на основе визуального анализа.
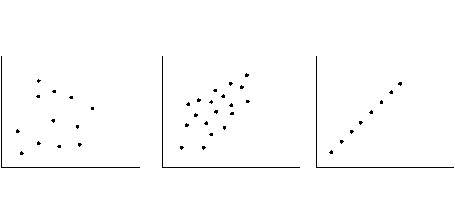
В научных исследованиях такая оценка неприемлема. Корелляционный анализ даёт возможность количественной объективной оценки.
Коэффициент корелляции – это число, указывающее на степень близости статистической зависимости к функциональной (rxy). Значения rx связаны с качественной оценкой. В предельном случае rxy=1 – функциональная связь; rxy=0 – отсутствие связи; rxy=1 – обратная функциональная связь. Рассмотрим графическое изображение статистической зависимости.
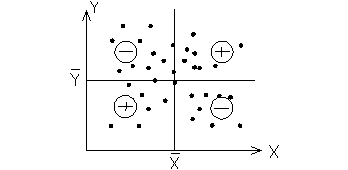
Место нахождения и мера отклонения отдельных точек от центра поля корелляции служит произведением 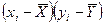 . Это произведение меняет свой знак в зависимости от расположения точек в квадранте. Если точки расположены симметрично и равномерно относительно центра, то:
. Это произведение меняет свой знак в зависимости от расположения точек в квадранте. Если точки расположены симметрично и равномерно относительно центра, то:
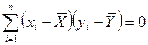
Непосредственно оценка корелляции с помощью такой суммы невозможна, поскольку она не нормирована и имеет размерность, поэтому для получения значения -1<rxy<1 эта сумма нормируется.
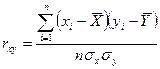
Значение rxy и качественные оценки:
rxy=0,3 – слабая корелляция; 0,3<rxy<0,5 – умеренная корелляция; 0,51<rxy≤0,8 – заметная корелляция; rxy>0,8 – высокая корелляция.
Близость коэффициента корелляции к 0 не всегда означает отсутствие корелляции, поскольку связь может быть нелинейной.
Оценка надёжности коэффициента корелляции
Коэффициент корелляции рассчитывается по ограниченному количеству точек, поэтому его значение может случайно принять либо очень высокое, либо очень маленькое значение, близкое к нулю, поэтому после вычисления коэффициента корелляции всегда делается оценка его надёжности. Критерий оценки – «гипотеза rxy=0». Эта оценка также основана на теории Стьюдена, в соответствии с которой вычисляется число:
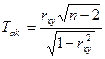
| K | α | ||
| 0,1 | 0,05 | 0,01 | |
| 0,8 | 0,87 | 0,95 | |
| 0,66 | 0,75 | 0,87 | |
| 0,54 | 0,63 | 0,76 | |
| 0,49 | 0,57 | 0,70 |
Это число сравнивают с табличным значением в зависимости от k=n-2 и α=1-Pдов.
Если Tkαвыч>Tkαтабл, то делается вывод, что вычисленный коэффициент корелляции надёжен и с вероятностью Pдов отличен от нуля – «нулевая гипотеза не подтверждается». Существует несколько методов оценки надёжности коэффициента корелляции:
1) Приведённый метод пригоден для небольшого количества экспериментальных точек, если их распределение заведомо подчинено нормальному закону.
Дата добавления: 2021-01-26; просмотров: 464;











