Оценка погрешности измерений
Измерение:
1) Процесс нахождения какой-либо величины опытным путём с применением технических средств.
2) Познавательный процесс сравнения величины чего-либо с известной величиной, принятой за эталон. Измерения бывают: а) статические; б) динамические; в) прямые; г) косвенные; д) особо точные; е) технические.
Задача оценки погрешности состоит в следующем: на вход в средство измерения подаётся значение измеряемой величины (a). На выходе мы имеем это значение с некоторой погрешностью. Погрешность бывает абсолютная (±ε) и относительная (Δ=±ε/a). Таким образом, непосредственно после измерений истинное значение a остаётся неизвестным. Задача состоит в оценке погрешности ε по сравнению со значением a.
Причины погрешности и их виды
Систематические погрешности остаются постоянными при повторных измерениях.
Причины систематических погрешностей:
1) Износ или повреждение приборов.
2) Неправильная установка прибора.
3) Воздействие внешней среды.
4) Субъективная погрешность.
5) Погрешность метода или схемы измерений.
Основной способ определения такой погрешности – измерение эталона.
Средства измерения должны отдаваться в специальный надзорный орган для поверки.
Случайные погрешности:
1) Трудно учитываемое влияние многих случайных факторов.
2) Грубые промахи.
Во время проведения экспериментальных исследований всегда возникают случайные погрешности, величину которых можно оценить методом статистического анализа на основе теории вероятностей.
Рассмотрим пример: в бассейне производится прогонка модели судна.
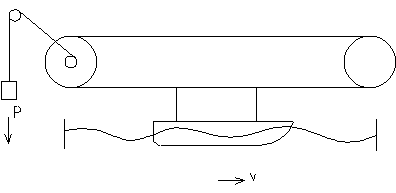
В результате 30 опытов были получены следующие значения:
| № | V | V | V |
| 1,7 | 1,7 | 1,8 | |
| 1,8 | 2,1 | 1,8 | |
| 1,8 | 2,0 | 1,8 | |
| 2,1 | 2,1 | 1,9 | |
| 1,8 | 1,9 | 1,6 | |
| 1,7 | 1,6 | 1,7 | |
| 1,9 | 1,9 | 1,8 | |
| 1,9 | 1,9 | 2,0 | |
| 1,7 | 1,9 | 1,6 | |
| 1,8 | 2,0 | 1,9 |
Простая обработка даёт результат: Vср=1,8
Размах результатов выборки: Vmax=2,1; Vmin=1,6
Без статистической обработки получим: V=1,8±0,5/2
ΔV=(Vmax-Vmin)/2=0,5
При использовании вероятностного метода учитывается то, что вероятность выпадения очень большого или очень маленького значения очень мала. При применении статистической погрешности в начале устанавливается закон распределения случайной величины. Для оценки закона распределения строится гистограмма – графическое представление частоты результатов в опыте.
| n | n/30 | |
| 1,6 | 0,1 | |
| 1,7 | 0,17 | |
| 1,8 | 0,27 | |
| 1,9 | 0,3 | |
| 2,0 | 0,1 | |
| 2,1 | 0,06 |
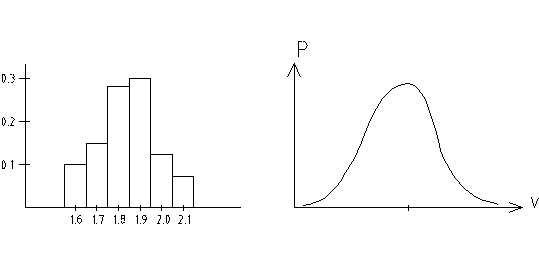
При этом относительная частота 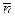 становится вероятностью, которая имеет вид формулы:
становится вероятностью, которая имеет вид формулы:
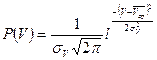
Основные характеристики закона:
1) Математическое ожидание: 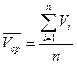
2) Дисперсия: 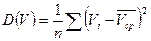
3) Среднее квадратическое отклонение: 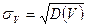
4) Среднее квадратическое отклонение среднего: 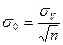
Погрешность измерений оценивается величиной доверительного интервала: 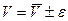
Доверительный интервал – это совокупность значений Vi, в интервал изменения которого попадает истинное значение V с заданной вероятностью Pзад. Соответственно, вероятность того, что Vi попадёт в интервал, называется доверительной вероятностью. Ширина доверительного интервала определяется по формуле: ε=±tσV, где t – гарантийный коэффициент. Вероятность попадания P в заданный интервал находится с помощью интеграла вероятности Лапласа.
Ф(1)=0,683; Ф(2)=0,955; Ф(3)=0,997.
В нашем примере 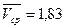 , σ=0,13.
, σ=0,13.
Таким образом, в интервал V=1,83±0,13 попадание составит 0,683; в интервал V=1,83±0,26 – 0,955; V=1,83±0,39 – 0,997.
Такие результаты достоверны, если число опытов превышает 50 при небольшой величине D или σ. Если n<50, то получается очень большая погрешность в определении σ и интервал случайно оказывается больше, чем есть на самом деле. Для малых выборок n=5 применяется метод Стьюдента (К. Госсег). Самое главное достоинство этого метода состоит в том, что математически доказано – ширину доверительного интервала можно определить по формуле:
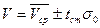
tст – гарантийный коэффициент Стьюдента.
| n | Фстдов |
| 2,77 | |
| 2,26 | |
| 2,09 | |
| 2,04 | |
| 2,0 |
Окончательно для скорости, определённой в опытах: V=1,83±2,04∙0,025
Без применения этой теории формула записывается: V=1,83±∙0,05; V=1,83±0,25
Оценка грубых промахов
Результат готовых измерений записывается в форме: 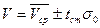
Грубые промахи очень сильно влияют, поэтому после проведения измерений следует выполнить поиск и устранение грубых промахов. Для быстрой оценки используют правило «трёх сигм». Последовательность действий:
1) Выбираются подозрительные значения из ряда измерений Vmin, Vmax.
2) Определяется Vср и σ.
3) Находится абсолютное отклонение.
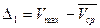 ;
; 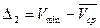
4) Δ1 и Δ2 сравниваются с 3σ.
Δ1>3σ, Δ2>3σ. Если выполняется одно из этих условий, соответствующие Vmax, Vmin удаляются из ряда измерений.
5) Производится окончательное определение 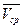 и σ.
и σ.
Этот метод очень груб и ненадёжен. Более точная оценка производится с помощью критерия Романовского. Этот критерий выведен на основе теории Стьюдента.
В критерии Романовского используется теорема о предельной ошибке (εпр≤tкрσ)
Если Δ>εпр, то результат выбраковывается из ряда.
| n Ф=> | 0,95 | 0,98 | 0,99 |
| 3,04 | 4,11 | 5,04 | |
| 2,37 | 2,96 | 3,41 | |
| 2,08 | 2,50 | 2,83 |
В нашем примере n=30; V=1,83; σ=0,13; Фдов=0,95; tкр=2,08.
Δ1=2,1-1,83=0,27; Δ2=1,83-1,6=0,23; σtк=0,27
Измерение V=2,1 – брак.
Поступая аналогичным образом, получим ряд из 25 чисел: σ=0,095; V=1,84; σ0=0,019; V=1,84±0,04.
Дата добавления: 2021-01-26; просмотров: 470;











