Б. Подбор сечения балки

1. Вариант сечения по рис. 7.12г

R = 200 10³ кПа; R_S = 100 10³ кПа.

А. Из условия прочности по нормальным напряжениям определяем требуемую величину осевого момента сопротивления.

Из эпюры изгибающих моментов получаем |M|_max = = 46,94 кН×м.

Допускаем, 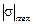= R и из этого условия определяем требуемое значение осевого момента сопротивления:

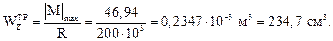
Определяем положение главной центральной оси Z и величину главного центрального момента инерции заданного сечения 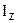(см. главу 5). Геометрические характеристики плоских сечений:

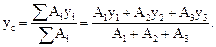
Здесь у_с – расстояние от произвольно взятой оси Z' до центральной оси Z для всей фигуры; А_i – площади отдельных фигур:

А₁ = 10δ × 2s = 20s²; А₂ = 22s×s = 22s²; А₃ = 5s×2s = 10s²;

у_i – ординаты центров тяжестей отдельных фигур относительно произвольно взятой оси Z'. Пусть произвольная ось Z' совпадает с осью Z₃ (см. рис. 7.12г).

у₁ = 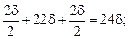у₂ =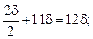

у₃ = 0, так как оси Z₃ и Z' совпадают.

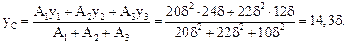
Отложим найденное расстояние y_Сот оси Z' и проведем общую центральную ось Z.

Осевой момент инерции всей фигуры относительно оси Z вычислим по формуле:

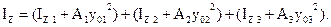
Здесь I_Zi – собственные моменты инерции простых фигур относительно их собственных центральных осей.

Так как все фигуры прямоугольники, то:

I_Z1 =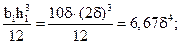

I_Z2 =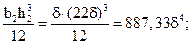

I_Z3 =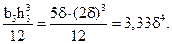

у_0i – расстояния от общей центральной оси Z до центральных осей простых фигур Z_i:

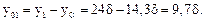
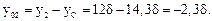
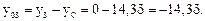
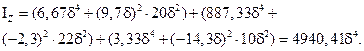
Б. Определим осевой момент сопротивления сечения.

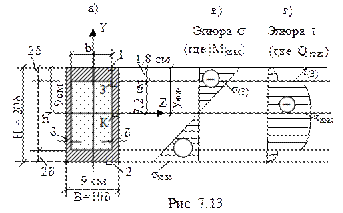
Расстояния от центральной (нейтральной) оси Z до наиболее удаленных (крайних) точек сечения А и В (рис. 7.13а):

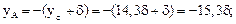
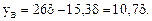
Отсюда: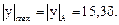

Осевой момент сопротивления определим по формуле:

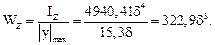
В. Приравняем найденное ранее значение требуемого осевого момента сопротивления к выражению для определения фактической величины осевого момента сопротивления и найдем параметр сечения d:

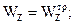
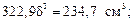
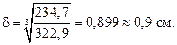
2. Расчет балки по 2-му варианту сечения (см. рис. 7.12д и 7.13а) R = 200М Па, R_S = 100 МПа.

А. Определение осевого момента сопротивления сечения

Так как сечение имеет две оси симметрии, его центр тяжести находится на их пересечении.

Определим главный центральный момент инерции сечения относительно оси Z как разность моментов инерции двух прямоугольников, центры тяжести которых совпадают.

I_Z =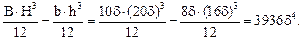

W_Z = 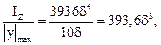здесь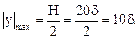

Б. Определение требуемого момента сопротивления сечения

Из условия прочности по нормальным напряжениям

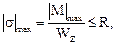при = R получаем

W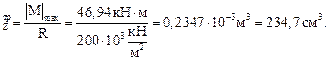

В. Из условия W_Z = W 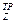определим размер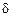

393,6 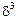= 234,7 см³;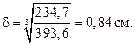

Полученное значение округляем по ГОСТ 103-76 для стальной полосы и принимаем 9 мм = 0,9 см.

Г. Проверим прочность подобранного сечения по нормальным и касательным напряжениям

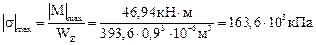<R.

Имеется недонапряжение из-за округления размера сечения в большую сторону. Оценим его в процентах:

(%) =

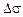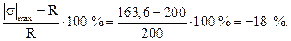
Из рис. 7.13г видно, что наибольшие касательные напряжения будут в точке К, лежащей на центральной оси.

Условие прочности:

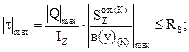
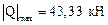(из эпюры Q, см. рис. 7.12б);

I_Z = 3936 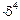= 3936 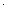0,9⁴ = 2582 см⁴;

в(у)_(к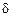) = 2 = 2 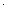0,9 = 1,8 см;

S 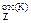находим как разность статических моментов площадей, лежащих выше центральной оси Z, относительно этой же оси:

S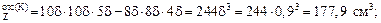

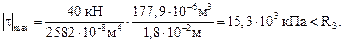
Условие прочности по касательным напряжениям выполняется с большим запасом.

ПРИМЕР 7.3

Для балки составного сечения (см. рис. 7.12г), рассчитанной в примере 7.2, требуется:

1. Выполнить полную проверку прочности балки при R = = 200 МПа, R_S = 100 МПа.

2. Подобрать размер сечения 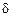по методу предельного равновесия (при коэффициенте запаса n = 1,2 и 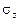= 240 МПа) и сравнить его с величиной, полученной по методу расчетных сопротивлений в примере 7.2.