II. Аксиомы вероятностей

Теперь мы сформулируем аксиомы, задающие само понятие вероятности.

1. Каждому событию 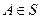поставлено в соответствии неотрицательное число Р(А), называемое вероятностью события А.

2. Если события 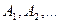попарно несовместны, то

.

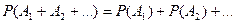Заметим, что при бесконечном числе событий 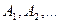в правой части написанного равенства стоит сумма ряда.

3. .

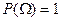Аксиомы 1-3 составляют основу всей теории вероятностей. Все теоремы этой теории выводятся из них формально логическим путем.

Схема, включающая в себя три объекта :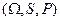

1. Множество Ω (называемое пространством элементарных событий),

2. Систему S подмножеств Ω (называемых событиями), удовлетворяющих аксиомам 1,2 пункта I,

3. Функцию Р(А), определенную на S и удовлетворяющую аксиомам 1,2,3 пункта II,

называется вероятностной схемой данного опыта (или вероятностным пространством данного опыта).

Упоминание об опыте может быть опущено, поскольку понятие вероятностной схемы является чисто математическим понятием и не требует привязывания к какому либо конкретному опыту.

С введением вероятностной схемы мы можем определить предмет теории вероятностей в более точных терминах, а именно:

теория вероятностей занимается изучением