Приближенное вычисление по формулам прямоугольников, трапеции, Симпсона

Сначала зададимся вопросом, а зачем вообще нужны приближенные вычисления? Вроде бы можно найти первообразную функции и использовать формулу Ньютона-Лейбница, вычислив точное значение определенного интеграла. В качестве ответа на вопрос сразу рассмотрим демонстрационный пример с рисунком.

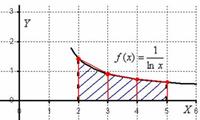
Вычислить определенный интеграл

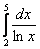
Всё было бы хорошо, но в данном примере интеграл не берётся – перед вами неберущийся, так называемый интегральный логарифм.

Существуют несколько основных методов приближенного вычисления определенного интеграла, который встречается в задачах:

Метод прямоугольников. Отрезок интегрирования разбивается на несколько частей и строится ступенчатая фигура, которая по площади близка к искомой площади:

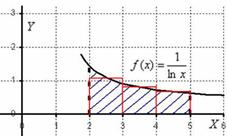
В данном примере проведено разбиение отрезка интегрирования 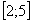на три отрезка:
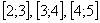. Очевидно, что чем чаще разбиение (больше более мелких промежуточных отрезков), тем выше точность.

Метод трапеций. Идея аналогична. Отрезок интегрирования разбивается на несколько промежуточных отрезков, и график подынтегральной функции приближается ломанойлинией:

Метод Симпсона (метод парабол). Это более совершенный способ – график подынтегральной функции приближается не ломаной линией, а маленькими параболками. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций.