Численное дифференцирование на основе интерполяционной формулы Ньютона

Запишем для функции f(x), заданной своими значениями в равноотстоящих узлах первый интерполяционный многочлен Ньютона:

Перепишем этот полином, производя перемножение скобок:

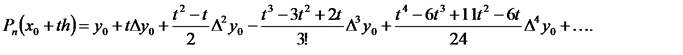
Дифференцируя 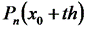по t , получим аналогично формуле (6.16):

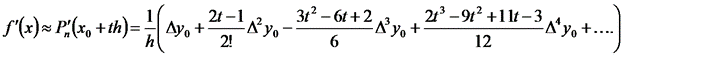(6.21)

Подобным путем можно получить и производные функции f(x) более высоких порядков. Однако каждый раз, вычисляя значение производной функции f(x) в фиксированной точке х, в качестве х₀ следует брать ближайшее слева узловое значение аргумента.

Формула (6.21) существенно упрощается, если исходным значением х оказывается один из узлов таблицы. Так как в этом случае каждый узел можно считать начальным, то принимая х=х_0, t=0, получаем:

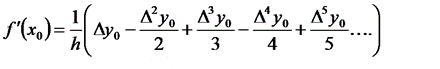
Эта формула позволяет точно получать значения производных функций, заданных таблично.

Выведем формулу погрешности дифференцирования. Используя формулу (6.17) применительно к первому интерполяционному многочлену Ньютона, запишем:

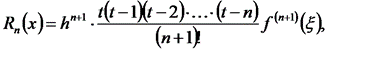
где 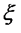‑ промежуточное значение между 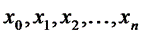и заданной точкой х. Предполагая, что f(x) дифференцируема п+1 раз, получим для оценки погрешности дифференцирования 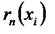(по аналогии с формулой (6.18)):

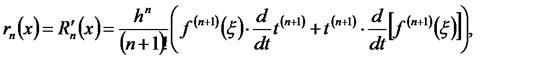
Для случая оценки погрешности в узле таблицы получим:

.

На практике 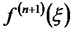оценивать непросто, поэтому при малых h приближенно полагают:

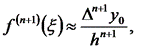
Что позволяет использовать приближенную формулу