Метод прямоугольников.

Вычислить определённый интеграл 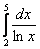приближённо:
а) методом левых прямоугольников;
б) методом правых прямоугольников.
Промежуток интегрирования разделить на 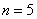равных отрезков, результаты вычислений округлять до 0,001

Решение: Вычислим шаг разбиения (длину каждого промежуточного отрезка):

Метод левых прямоугольников получил своё называние из-за того,

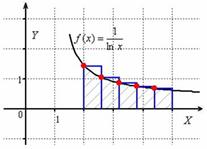
что высОтыпрямоугольников на промежуточных отрезках равны значениям функции в левых концах данных отрезков:
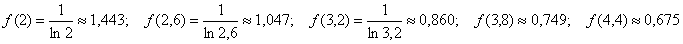Ни в коем случае не забываем, что округление следует проводить до трёх знаков после запятой – это существенное требование условия.

Вычислим площадь ступенчатой фигуры, которая равна сумме площадей прямоугольников:

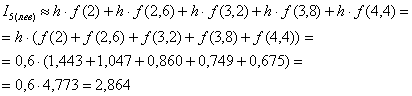
Таким образом, площадь криволинейной трапеции: 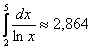. Совершенно понятно, что, рассмотрев бОльшее количество промежуточных отрезков (измельчив разбиение), ступенчатая фигура будет гораздо больше похожа на криволинейную трапецию, и мы получим лучший результат.

При использовании «правого» метода высОты прямоугольников равны значениям функциив правых концах промежуточных отрезков:

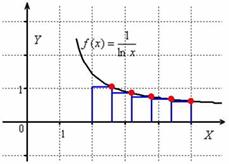
Вычислим недостающее значение 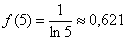и площадь ступенчатой фигуры:

– тут, что и следовало ожидать, приближение сильно занижено:

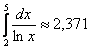
Запишем формулы в общем виде. Если функция 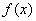непрерывна на отрезке 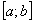, и он разбит на 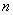равных частей: 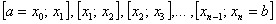, то определённый интеграл 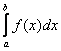можно вычислить приближенно по формулам:
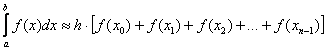– левых прямоугольников;
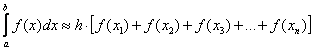– правых прямоугольников;
(формула в следующей задаче) – средних прямоугольников,
где 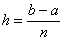– шаг разбиения.

В чём их формальное различие? В первой формуле нет слагаемого 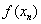, а во второй -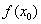

На практике рассчитываемые значения 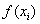удобно заносить в таблицу: