Вычисление двойного интеграла в полярной
Системе координат
Осуществим в двойном интеграле 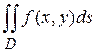 , заданном в декартовой системе координат, замену переменных по формулам перехода к полярной системе координат:
, заданном в декартовой системе координат, замену переменных по формулам перехода к полярной системе координат: 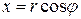 ,
, 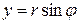 . В этом случае подынтегральная функция будет зависеть от полярных координат
. В этом случае подынтегральная функция будет зависеть от полярных координат 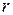 и
и 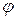 :
: 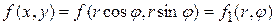 . Пусть область
. Пусть область 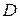 такова, что любой луч, выходящий из начала координат и проходящий через внутреннюю точку области, пересекает границу
такова, что любой луч, выходящий из начала координат и проходящий через внутреннюю точку области, пересекает границу 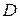 не более, чем в двух точках . Линии, ограничивающие область
не более, чем в двух точках . Линии, ограничивающие область 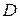 , имеют уравнения
, имеют уравнения 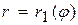 ,
, 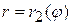 , где
, где 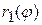
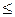
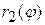 ,
, 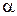
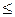
 . Такую область, применительно к полярной системе координат, будем называть правильной (см. рис.).
. Такую область, применительно к полярной системе координат, будем называть правильной (см. рис.).
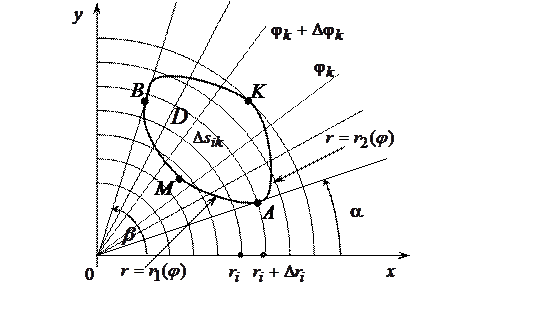
Поскольку предел интегральной суммы не зависит от способа разбиения фигуры на элементарные, подобное разбиение можно осуществить с помощью лучей 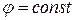 , проходящих через начало координат, и концентрических окружностей
, проходящих через начало координат, и концентрических окружностей 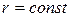 с центрами в начале координат. При пересечении двух окружностей радиусов
с центрами в начале координат. При пересечении двух окружностей радиусов 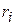 ,
, 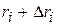 и лучей, проведенных под углами
и лучей, проведенных под углами 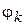 и
и 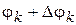 , образуется элементарная криволинейная фигура
, образуется элементарная криволинейная фигура 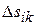 . Ее, с точностью до бесконечно малых высшего порядка, можно рассматривать как прямоугольник со сторонами
. Ее, с точностью до бесконечно малых высшего порядка, можно рассматривать как прямоугольник со сторонами 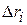 , и
, и 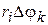 , площадь которого
, площадь которого 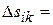
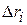
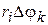 .
.
Следовательно, двойной интеграл в полярных координатах имеет вид
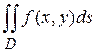
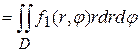 .
.
Итак, если область 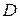 является правильной применительно к полярным координатам, то вычисление двойного интеграла сводится к вычислению двукратного интеграла по переменным
является правильной применительно к полярным координатам, то вычисление двойного интеграла сводится к вычислению двукратного интеграла по переменным 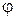 и
и 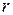 . Для расстановки пределов интегрирования из полюса проводят ограничивающие лучи
. Для расстановки пределов интегрирования из полюса проводят ограничивающие лучи 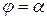 и
и 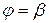 , записывают уравнения линий входа в область (AMВ) —
, записывают уравнения линий входа в область (AMВ) — 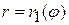 и выхода из нее (АКВ) —
и выхода из нее (АКВ) — 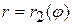 . Тогда
. Тогда 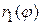
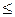
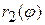 ,
, 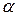
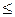
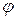
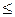
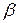 .
.
Как правило, внешний интеграл вычисляется по переменной 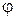 , а внутренний — по
, а внутренний — по 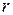 . На основании изложенного имеет место следующая формула вычисления двойного интеграла в полярных координатах:
. На основании изложенного имеет место следующая формула вычисления двойного интеграла в полярных координатах:
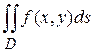
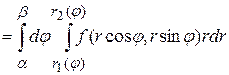 ,
,
при этом лучи 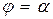 и
и 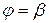 , и кривые
, и кривые 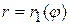 ,
, 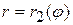 ограничивают фигуру
ограничивают фигуру 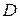 , по которой осуществляется вычисление двойного интеграла.
, по которой осуществляется вычисление двойного интеграла.
Пример.Вычислить двойной интеграл 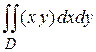 по области
по области 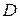 , ограниченной линиями:
, ограниченной линиями: 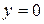 ,
, 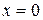 ,
, 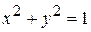 ,
, 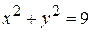 .
.
Решение. Изобразим на рисунке заданную область интегрирования.
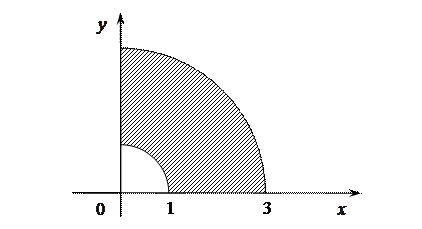
Если рассматривать данную область как стандартную относительно оси 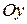 , то область интегрирования необходимо разбить на две области, а повторный интеграл представить как сумму двух интегралов, так как снизу функция
, то область интегрирования необходимо разбить на две области, а повторный интеграл представить как сумму двух интегралов, так как снизу функция 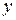 выражена двумя аналитическими выражениями (
выражена двумя аналитическими выражениями ( 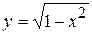 и
и 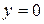 ), то область интегрирования необходимо разбить на две области, а повторный интеграл представить как сумму двух интегралов. Аналогичная ситуация возникнет и для оси
), то область интегрирования необходимо разбить на две области, а повторный интеграл представить как сумму двух интегралов. Аналогичная ситуация возникнет и для оси 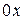 . При этом, как и в первом случае, так и во втором мы придем к необходимости нахождения достаточно сложных интегралов. Так как линиями, частично ограничивающими область
. При этом, как и в первом случае, так и во втором мы придем к необходимости нахождения достаточно сложных интегралов. Так как линиями, частично ограничивающими область  , являются окружности, имеет смысл перейти к полярной системе координат.
, являются окружности, имеет смысл перейти к полярной системе координат.
Перейдем к полярным координатам по формулам:
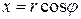 ,
, 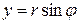 .
.
Тогда уравнение 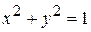 в полярных координатах запишется в виде:
в полярных координатах запишется в виде:
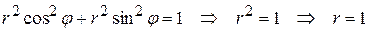 .
.
Уравнение 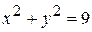 получит вид:
получит вид:
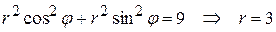 .
.
Ограничение 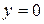 в полярных координатах будет иметь вид:
в полярных координатах будет иметь вид:
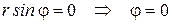 .
.
Аналогично 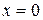
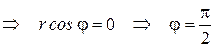 .
.
Подынтегральная функция 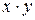 примет вид:
примет вид: 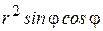 .
.
Область 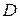 является правильной применительно к полярным координатам, следовательно, можем использовать формулу:
является правильной применительно к полярным координатам, следовательно, можем использовать формулу:
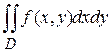
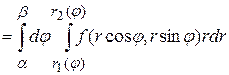 .
.
Получаем:
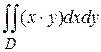
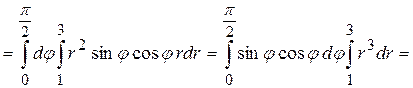
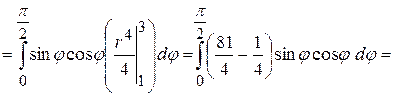
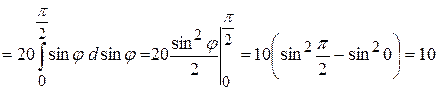 .
.
Тройной интеграл
По аналогии с двойным интегралом вводится понятие тройного интеграла. Рассмотрим ограниченную замкнутую пространственную область 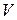 и определенную в ней непрерывную функцию
и определенную в ней непрерывную функцию 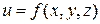 . Область
. Область 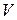 разобьем на
разобьем на 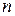 элементарных пространственных областей
элементарных пространственных областей 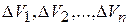 . Предполагается, что область
. Предполагается, что область 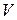 и элементарные области
и элементарные области 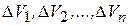 имеют объемы, которые будем обозначать соответственно теми же символами. В каждой элементарной области
имеют объемы, которые будем обозначать соответственно теми же символами. В каждой элементарной области 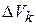 (
( 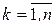 ) выберем произвольную точку
) выберем произвольную точку 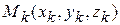 , значение функции в этой точке
, значение функции в этой точке 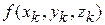 умножим на объем элементарной области
умножим на объем элементарной области 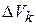 и составим сумму всех таких произведений:
и составим сумму всех таких произведений:
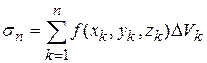 ,
,
которая называется интегральной суммой данной функции по данному объему.
Обозначим через 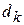 диаметр области
диаметр области 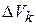 . Пусть
. Пусть 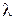 — наибольший из этих диаметров. И перейдем в последнем равенстве к пределу при
— наибольший из этих диаметров. И перейдем в последнем равенстве к пределу при 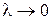 .
.
Если предел интегральной суммы существует, то он и называется тройным интегралом от функции 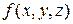 по пространственной области
по пространственной области 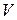 .
.
Итак, по определению
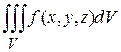
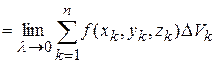 . (1)
. (1)
Тройной интеграл от функции 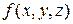 по пространственной области
по пространственной области 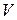 также обозначается следующим образом:
также обозначается следующим образом:
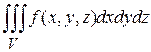 .
.
Отметим без доказательства, что если функция 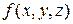 непрерывна в рассматриваемой замкнутой области
непрерывна в рассматриваемой замкнутой области 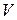 , то предел в правой части формулы (1) существует и не зависит от способа разбиения области
, то предел в правой части формулы (1) существует и не зависит от способа разбиения области 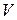 на элементарные и выбора точки
на элементарные и выбора точки 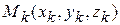 в элементарной области
в элементарной области 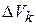 .
.
Предположим, что в области 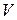 распределено вещество, объемная плотность которого задана непрерывной функцией
распределено вещество, объемная плотность которого задана непрерывной функцией 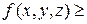
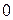 , тогда произведение
, тогда произведение 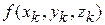
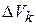 выражает приближенную массу элементарной области
выражает приближенную массу элементарной области 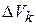 , интегральная сумма — приближенную массу всей области
, интегральная сумма — приближенную массу всей области 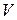 , а тройной интеграл — точное значение этой массы, т. е.
, а тройной интеграл — точное значение этой массы, т. е.
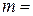
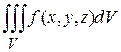 .
.
Данная формула выражает механический смысл тройного интеграла: тройной интеграл представляет массу, заполняющую область интегрирования 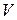 .
.
Если в формуле 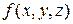
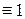 , то
, то 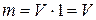 мы получаем формулу для вычисления объема с помощью тройного интеграла:
мы получаем формулу для вычисления объема с помощью тройного интеграла:
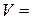
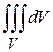 или
или 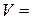
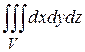
Тройной интеграл обладает свойствами, аналогичными свойствам двойного интеграла.
Перейдем к вопросу о вычислении тройного интеграла в прямоугольных декартовых координатах. Предположим, что область 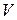 является стандартной в направлении оси
является стандартной в направлении оси 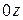 , т. е. удовлетворяющей следующим условиям:
, т. е. удовлетворяющей следующим условиям:
1) всякая прямая, параллельная этой оси и имеющая с данной областью общие точки, пересекает границу области только в двух точках;
2) проекция 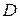 области
области 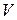 на плоскость
на плоскость 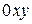 представляет собой стандартную область в направлении оси
представляет собой стандартную область в направлении оси 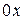 или оси
или оси 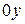 .
.
Пусть стандартная область 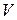 ограничена сверху поверхностью
ограничена сверху поверхностью 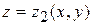 , снизу — поверхностью
, снизу — поверхностью 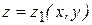 , тогда можно показать, что
, тогда можно показать, что
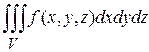
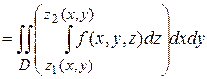 .
.
Если область 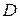 является стандартной в направлении оси
является стандартной в направлении оси 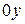 и определяется неравенствами
и определяется неравенствами 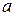
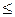
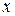
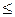
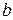 ,
, 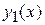
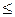
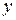
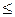
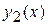 , то
, то
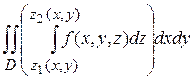
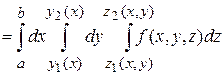 .
.
Следовательно, в этом случае
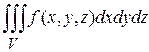
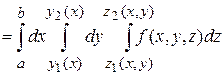 .
.
Замечание. Если область 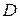 является стандартной в направлении оси
является стандартной в направлении оси 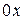 и определяется неравенствами
и определяется неравенствами 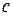
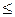
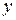
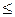
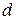 ,
, 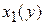
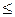
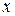
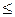
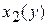 , то
, то
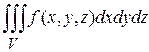
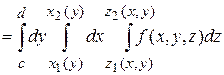 .
.
Замечание. Если область  является стандартной в направлении каждой координатной оси и ее проекции на координатные плоскости являются стандартными в направлении каждой соответствующей оси, то пределы интегрирования в трехкратном интеграле можно расставить шестью различными способами.
является стандартной в направлении каждой координатной оси и ее проекции на координатные плоскости являются стандартными в направлении каждой соответствующей оси, то пределы интегрирования в трехкратном интеграле можно расставить шестью различными способами.
Пример.Вычислить тройной интеграл 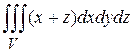 по области
по области 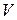 , ограниченной поверхностями
, ограниченной поверхностями 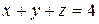 ,
, 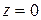 ,
, 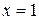 ,
, 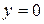 ,
, 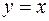 ,.
,.
Решение.Изобразим область 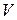 .
.

Эта область является стандартной в направлении оси 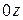 , а проекция
, а проекция 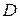 области
области 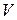 на плоскость
на плоскость 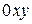 представляет собой стандартную область в направлении оси
представляет собой стандартную область в направлении оси 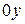 . Следовательно,
. Следовательно,
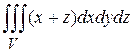
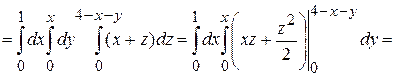
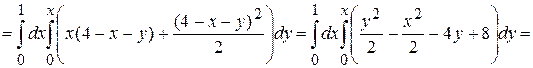
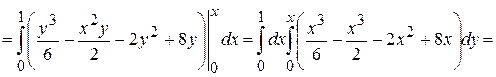
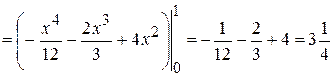 .
.
Пример.Найти объем тела, ограниченного поверхностями 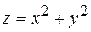 ,
, 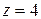 .
.
Решение. Уравнения поверхностей, ограничивающих тело имеют наиболее простой вид в цилиндрических координатах, связь которых с декартовыми осуществляется по формулам:
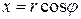 ,
, 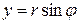 ,
, 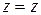 .
.
Первая поверхность являющаяся параболоидом вращения примет вид:
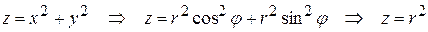 .
.
Уравнение плоскости 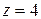 в цилиндрических координатах останется без изменений.
в цилиндрических координатах останется без изменений.
Изобразим тело, объем которого необходимо найти, на рисунке.

Решая совместно уравнения 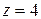 и
и 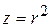 , получаем, что область
, получаем, что область 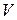 проектируется в плоскость
проектируется в плоскость 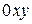 в круг
в круг 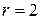 .
.
Следовательно,

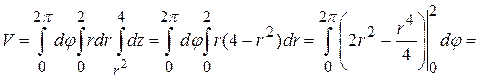
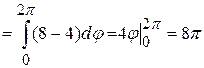 .
.
Дата добавления: 2021-01-11; просмотров: 570;











