Особенность задачи численного дифференцирования
Когда производную аналитически заданной функции по причине ее сложности искать затруднительно либо выражение для производной приобретает неудобную для применения форму, используется приближенное или численное дифференцирование. Этот метод тем более необходим, если исходная функция задана таблично. Один из способов решения задачи дифференцирования – использование интерполяционных многочленов.
Пусть f(x) – функция, для которой нужно найти производную в заданной точке отрезка [a;b], Fn(x) – интерполяционный многочлен для f(x), построенный на отрезке [a;b]. Заменяя f(x) интерполяционным многочленом Fn(x), получим значение производной f(x) на отрезке [a;b] как значение производной 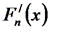 интерполяционного многочлена, т.е. примем приближенно
интерполяционного многочлена, т.е. примем приближенно
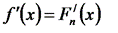 (6.5)
(6.5)
Аналогичным путем можно поступать при нахождении значений производных высших порядков функции f(x).
Полагая, что погрешность интерполирования определяется формулой
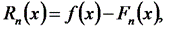 (6.6)
(6.6)
Получаем подход к оценке погрешности производной 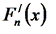 :
:
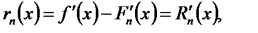 (6.7)
(6.7)
Т.е. погрешность производной интерполирующей функции равна производной от погрешности этой функции.
Рассмотрим методы численного дифференцирования на основе интерполяционных многочленов Ньютона.
Применяя для численного дифференцирования на отрезке [a;b] интерполяционный полином, естественно строить на этом отрезке систему равноотстоящих узлов
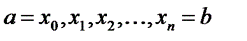 ,
,
Которыми отрезок делится на п равных частей: 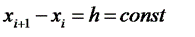 (i=0, 1, 2, п‑1).
(i=0, 1, 2, п‑1).
В этом случае шаг интерполирования равен 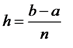 , положим
, положим 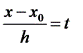
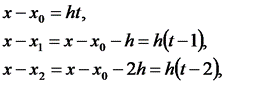
Дата добавления: 2021-01-26; просмотров: 610;











