Моделирование случайных событий

Для моделирования случайного события А, вероятность которого равна Р_с, достаточно сформировать одно число r, равномерно распределенное на интервале (0,1). При попадании r в интервал (0,Р_с) считают, что событие А наступило, в противном случае не наступило.

Пусть, например, вероятность отказа вычислительной системы составляет 0,3. Чтобы определить, возникнет ли отказ на очередном шаге моделирования, достаточно сгенерировать с помощью датчика одно случайное число r и сравнить его с вероятностью отказа (рис.2.4).

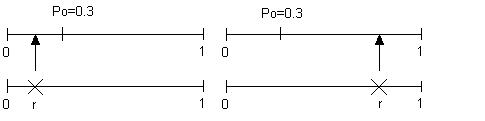
Рисунок 2.4 - Моделирование случайного события; отказ «произошел» (слева), отказ «не произошел» (справа)

Для моделирования полной группы N несовместных событий А={А₁, А₂,…, А_N} с вероятностями соответственно 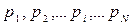также достаточно одного значения r: событие А_i из группы А считается наступившим, если выполняется условие:

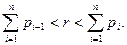
Здесь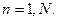

Предположим, что в каждый момент времени может происходить обращение только к одному из трех модулей оперативной памяти вычислительной системы. Вероятности обращения к каждому из них 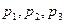равны соответственно 0.3, 0.5 и 0.2. Чтобы узнать, из какого именно модуля будут считаны данные, необходимо определить, в какой интервал попадет полученное от датчика случайное число r (рис.2.5).

Что будет если сумма вероятностей меньше 1?

Ответ.

Если группа событий А не полна, то вводят фиктивное событие А_N+1 с вероятностью p_N+1 такой, что сумма вероятностей становится равной 1. После этого генерируют число r и проверяют указанное выше условие. При А=А_N+1 считают, что ни одно событие из исходной группы А не наступило.

Для имитации зависимых событий А и В (В зависит от А) необходимо знать безусловную вероятность p(А) события А и условные вероятности p(В/А) и p(В/Ā). Сначала описанным выше способом имитируется появление события А, в зависимости от исхода выбирается одна из вероятностей p(В/А) или p(В/Ā), и по той же технологии определяется наступление события В.

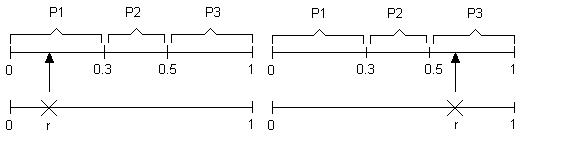
Рисунок 2.5 - Моделирование полной группы из трех несовместных событий – обращение к первому модулю памяти (слева), обращение к третьему модулю памяти (справа)