Характеристика методов моделирования вероятностных объектов

Вероятностным объектом называют систему, находящуюся под воздействием случайных внешних или внутренних факторов: возмущений и помех. Они могут быть как непрерывными величинами или функциями, так и дискретными. При анализе функционирования таких систем возникают различные вероятностные задачи, например, определение математического ожидания, дисперсии, корреляционной функции, спектральной плотности реакции системы по математическому ожиданию, дисперсии, корреляционной функции, спектральной плотности воздействия на систему.

Аналитическое решение такой задачи возможно лишь в отдельных случаях, чаще приходится прибегать к имитационному моделированию на ЭВМ. При этом возможны два метода решения этих задач: детерминированный и статистический. Детерминированный метод предполагает моделирование аналитических соотношений между вероятностными характеристиками входного воздействия и реакции системы. Задача решается путем детерминированного преобразования вероятностной характеристики воздействия в одноименную вероятностную характеристику реакции. Метод имеет ограниченное применение.

Статистический методпредполагает моделирование системы, находящейся под влиянием случайных факторов. Задача решается путем статистической обработки результатов исследования модели. Метод является универсальным, поскольку применим и к детерминированным задачам. В этом случае производится замена детерминированной задачи эквивалентной схемой некоторой вероятностной системы, выходные характеристики которой совпадают с решением детерминированной задачи. В результате точное решение задачи заменяется приближенным. Однако с ростом числа испытаний погрешности оценок уменьшаются. При достаточно большом числе испытаний полученные результаты приобретают статистическую устойчивость и с определенной точностью могут быть приняты в качестве оценок неизвестных характеристик системы.

Накопление значительного количества данных о выходных характеристиках вероятностной системы осуществляют в ходе статистического эксперимента с моделью. Под статистическим экспериментом обычно понимают постановку опытов с моделью системы и наблюдение за поведением модели при случайных воздействиях. Для его осуществления имитационная модель должна отражать логику функционирования системы во времени и обеспечивать возможность многократного повторения опытов с одновременным накоплением и статистической обработкой данных.

В основе статистического эксперимента лежит метод статистических испытаний (метод Монте-Карло). Суть его состоит в том, что результат испытания зависит от значения некоторой случайной величины, распределенной по заданному закону. Поэтому результат каждого отдельного испытания также носит случайный характер. Проведя серию испытаний, получают множество частных значений наблюдаемой характеристики (выборку). Полученные статистические данные обрабатываются и представляются в виде численных оценок интересующих исследователя величин (характеристик системы).

Теоретической основой метода статистических испытаний являются предельные теоремы теории вероятностей (теорема Чебышева, теорема Бернулли, теорема Пуассона). Принципиальное значение предельных теорем состоит в том, что они гарантируют высокое качество статистических оценок при весьма большом числе испытаний.

В качестве примера рассмотрим применение метода статистических испытаний для вычисления площади круга заданного радиуса[3]. Данная задача явно относится к классу детерминированных задач. Пусть круг имеет радиус r=5, и его центр находится в точке с координатами (1,2). Уравнение соответствующей окружности имеет вид:

.

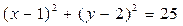Для решения задачи методом Монте-Карло впишем круг в квадрат. Его вершины будут иметь координаты (-4,-3), (-4,7), (6,7). Любая точка внутри квадрата или на его границе должна удовлетворять неравенствам -4<x<6 и -3<y<7.При решении задачи естественно исходить из того, что все точки в этом квадрате могут появляться с одинаковой вероятностью, то есть x и y распределены равномерно со следующими плотностями вероятности:

f(x)=1/10 для -4≤x≤6 и f(x)=0 – в противном случае;

f(y)=1/10 для -3≤y≤7 и f(y)=0 – в противном случае.

Проведя некоторое количество испытаний (то есть, получив множество случайных точек, принадлежащих квадрату), подсчитаем число точек, попавших внутрь круга или на окружность. Если выборка состоит из n наблюдений и m точек попали внутрь круга, то оценку площади круга можно получить из соотношения:

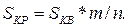
В табл.2.1. приведены оценки S_кр, полученные для разных значений n, причем для каждого n выполнялось 5 прогонов (точное значение S_кр = 78,54 см).Прогоны отличаются друг от друга последовательностями случайных чисел, из которых формировались координаты точек (рис.3.1).

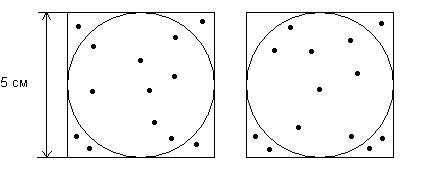
Рисунок 2.1-Различные результаты двух прогонов при неизменном количестве точек (n=13). Слева показан результат первого прогона, справа – второго.

На основании полученных результатов могут быть сделаны выводы, которые справедливы для любого имитационного эксперимента независимо от физической природы и типа моделируемой системы:

каждый прогон модели можно рассматривать как одно наблюдение в проводимом эксперименте на модели;

Таблица 2.1- Результаты статистических испытаний

---------------------------------------------------------------------------------------------------