Этапы имитационного моделирования системы
Процесс имитационного моделирования сложной системы S можно разделить на три этапа:
1. Построение математической модели 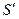 .
.
2. Разработка моделирующего алгоритма и построение имитационной модели 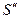 .
.
3. Исследование системы S с помощью модели 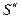 , то есть проведение имитационных экспериментов, обработка и интерпретация результатов.
, то есть проведение имитационных экспериментов, обработка и интерпретация результатов.
Между этапами существует и обратная связь, обеспечивающая уточнение, корректировку и учет дополнительной информации при разработке и использовании имитационной модели.
Этап 1. На основании изучения содержательного описания системы S осуществляется переход к математической модели 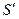 . Построение модели
. Построение модели 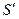 включает пять шагов.
включает пять шагов.
Постановка задачи и формулировка целей исследования.
Анализ системы 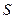 , который заключается в разбиении (декомпозиции) системы на элементы и определении связей между элементами.
, который заключается в разбиении (декомпозиции) системы на элементы и определении связей между элементами.
Определение параметров, переменных и пространства состояний системы 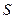 , то есть характеристик
, то есть характеристик 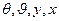 ; установление областей для каждой характеристики.
; установление областей для каждой характеристики.
Выбор показателей эффективности функционирования (вектора 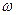 ).
).
Описание модели 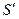 системы
системы 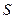 и проверка ее адекватности: использование математических моделей типа ДД, НД, ДВ, НВ; проверка гипотез, предложений и математических соотношений.
и проверка ее адекватности: использование математических моделей типа ДД, НД, ДВ, НВ; проверка гипотез, предложений и математических соотношений.
Этап 2. Здесь осуществляется переход от модели 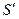 к моделирующему алгоритму и имитационной модели
к моделирующему алгоритму и имитационной модели 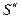 . Этот переход включает пять шагов.
. Этот переход включает пять шагов.
2.1 Выбор способа имитации, вычислительных и программных средств реализации ИМ.
Построение логической схемы моделирующего алгоритма.
Алгоритмизация математических моделей, описывающих поведение элементов системы и связей между ними.
Разработка имитационной модели, то есть программирование моделирующего алгоритма.
Отладка, тестирование и проверка адекватности ИМ.
Этап 3. Использование ИМ, которое включает три шага.
3.1 Планирование имитационных экспериментов.
3.2 Проведение имитационных экспериментов.
3.3 Обработка, анализ и интерпретация результатов моделирования.
Остановимся подробнее на шагах 3.1–3.3. Пусть моделируемая на интервале 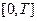 система
система 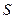 характеризуется вектором параметров
характеризуется вектором параметров 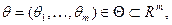 значениями которого в ИМ можно управлять, и вектором показателей эффективности (ПЭ) функционирования на интервале
значениями которого в ИМ можно управлять, и вектором показателей эффективности (ПЭ) функционирования на интервале 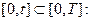
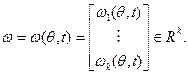
В результате имитационного моделирования системы 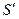 при заданных значениях вектора
при заданных значениях вектора 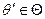 и
и 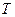 получают:
получают:
фазовую траекторию системы 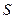
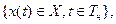 (2.4)
(2.4)
где 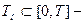 конечное множество моментов изменения модельного времени, получаемое по принципам «
конечное множество моментов изменения модельного времени, получаемое по принципам « 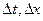 », причем
», причем 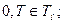
значения показателей эффективности для каждого интервала модельного времени 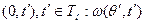 и для всего интервала моделирования в целом
и для всего интервала моделирования в целом
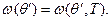 (2.5)
(2.5)
Имитационные модели используются для решения различных задач исследования сложных систем.
Задача 1. Оценивание значений показателей эффективности 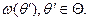
Задача 2. Оценивание функциональной зависимости 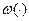 от
от 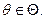
Задача 3. Сравнение эффективности функционирования системы 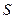 для различных значений параметров
для различных значений параметров 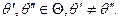
Задача 4. Оптимизация системы 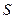 на множестве
на множестве 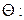
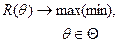
где 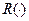 – некоторый критерий оптимальности (обобщенный скалярный показатель эффективности) для системы
– некоторый критерий оптимальности (обобщенный скалярный показатель эффективности) для системы 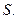
Выбор значений параметров 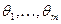 определяется целью имитационных экспериментов.
определяется целью имитационных экспериментов.
Процесс задания значений 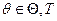 и способа формирования выборки
и способа формирования выборки 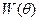 значений ПЭ, обеспечивающих эффективное решение задач исследования сложной системы
значений ПЭ, обеспечивающих эффективное решение задач исследования сложной системы 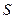 , называют планированием имитационных экспериментов.
, называют планированием имитационных экспериментов.
Необходимость этапа 3.3 покажем для случая, когда выборка значений ПЭ получается в результате серии независимых прогонов ИМ.
ИЭ с моделью системы 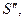 в результате которого для заданных значений
в результате которого для заданных значений 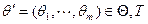 имитируется фазовая траектория
имитируется фазовая траектория 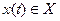 и вычисляются показатели эффективности (2.5), называется прогоном ИМ.
и вычисляются показатели эффективности (2.5), называется прогоном ИМ.
В результате одного прогона ИМ 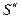 получают одну реализацию показателя эффективности
получают одну реализацию показателя эффективности 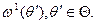 По одной случайной реализации ПЭ нельзя судить об эффективности функционирования системы
По одной случайной реализации ПЭ нельзя судить об эффективности функционирования системы 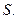 Поэтому на этапе 3.2 для заданных значений
Поэтому на этапе 3.2 для заданных значений 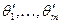 (т.е. для заданных значений
(т.е. для заданных значений 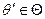 ), осуществляется
), осуществляется 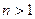 прогонов ИМ, в результате которых получается случайная выборка значений ПЭ
прогонов ИМ, в результате которых получается случайная выборка значений ПЭ
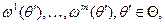
где 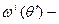 значение ПЭ функционирования системы
значение ПЭ функционирования системы 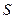 для
для 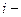 го (
го ( 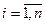 ) прогона ИМ.
) прогона ИМ.
Для оценивания эффективности функционирования системы по случайной выборке 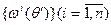 необходим этап 3.3 – этап обработки, анализа и интерпретации результатов имитационного моделирования. На этом этапе используются методы статического анализа данных.
необходим этап 3.3 – этап обработки, анализа и интерпретации результатов имитационного моделирования. На этом этапе используются методы статического анализа данных.
Пусть моделирующий алгоритм построен по принципу « 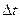 »:
»:
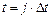
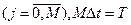 ,
,
а целью имитационного эксперимента является решение задачи 4, где 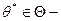 искомое оптимальное значение вектора параметров. Тогда процесс ИЭ с моделью системы S можно представить в виде схемы (рис. 2.7).
искомое оптимальное значение вектора параметров. Тогда процесс ИЭ с моделью системы S можно представить в виде схемы (рис. 2.7).
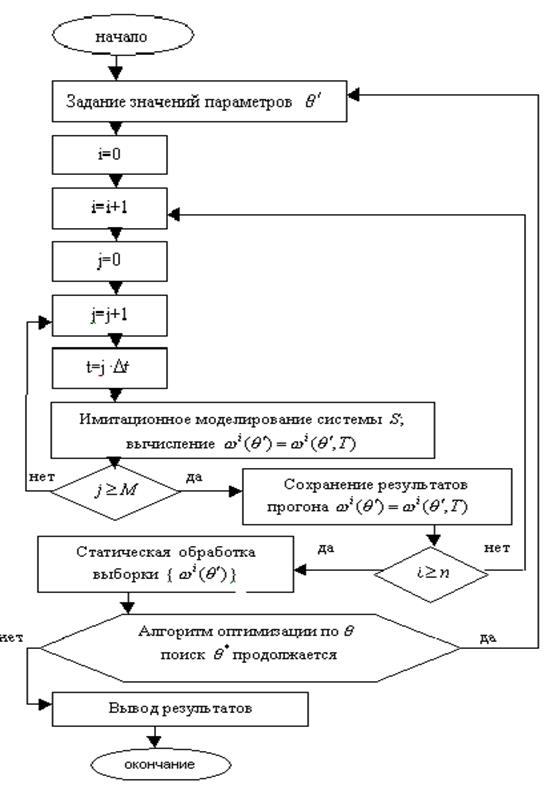 |
Рисунок 2.7 - Схема алгоритма имитационного эксперимента
Дата добавления: 2016-10-18; просмотров: 2859;











