Формирование базовой последовательности случайных чисел

Поскольку имитационная модель позволяет исследовать поведение различных систем с учетом влияния случайных факторов, то эти факторы, в зависимости от их природы, могут быть отражены в модели как случайные события, случайные величины (дискретные или непрерывные) или как случайные функции (процессы).

Например, если с помощью создаваемой имитационной модели предполагается исследовать надежность вычислительной системы, то возникновение отказа будет представлено в модели как случайное событие. Если же модель предназначена для оценки временных параметров процесса обслуживания клиентов в банке, то интервал времени до появления очередного клиента удобнее всего описать как случайную величину, распределенную по некоторому закону.

Методы генерации случайных чисел.В основе всех методов и приемов моделирования случайных факторов лежит использование случайных чисел имеющих равномерное распределение на интервале (0,1).

«Истинно» случайные числа формируются с помощью аналого-цифровых преобразователей на основе сигналов физических генераторов, использующих естественные источники случайных шумов (радиоактивный распад, шумы электронных и полупроводниковых устройств и т.п.).

Случайные числа, генерируемые аппаратно или программно на ЭВМ, называются псевдослучайными. Однако их статистические свойства совпадают со статистическими свойствами «истинно» случайных чисел. В состав практически всех современных систем программирования входят специальные функции генерации случайных чисел, которые обычно называют датчиками или генераторами случайных чисел.

Наиболее простой метод программной генерации случайных чисел – мультипликативный; в его основе лежит следующее рекуррентное соотношение:

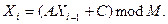
Здесь X_i, X_i-1 – очередное и предыдущее случайные числа соответственно; А, С – константы; М – достаточно большое целое положительное число (чем больше M, тем длиннее неповторяемая последовательность).

Достоинство метода заключается в том, что при одних и тех же значениях параметров, входящих в это выражение, можно полностью воспроизвести эксперимент.

Требования к генераторам случайных чисел.Практика показывает, что результаты имитационного моделирования существенно зависят от качества используемых последовательностей псевдослучайных чисел. Поэтому применяемые в имитационных моделях генераторы случайных чисел должны быть проверены на пригодность. При этом оценивают равномерность, случайность и независимость последовательности. Рассмотрим методы проведения такого анализа, наиболее часто применяемые на практике.

Проверка равномерности может быть выполнена с помощью гистограммы относительных частот генерируемой случайной величины. Для ее построения интервал (0,1) разбивается на m равных частей и подсчитывается относительное число попаданий значений случайной величины в каждый интервал. Чем ближе огибающая гистограммы к прямой параллельной оси y, тем в большей степени, генерируемая последовательность отвечает требованию равномерности распределения (рис.3.3.).

Проверка случайности. Рассмотрим один из основных методов проверки – метод комбинаций. Суть его сводится к следующему. Выбирают достаточно большую последовательность случайных чисел Х_i и для нее определяют вероятность появления в каждом из Х_i ровно j единиц. При этом могут анализироваться как все разряды числа, так и только i старших. Теоретически закон появления j единиц в i разрядах двоичного числа может быть описан как биномиальный закон распределения (исходя из независимости отдельных разрядов).

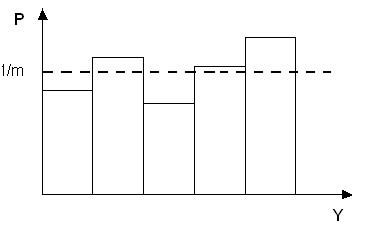
Рисунок 2.3 - Гистограмма относительных частот последовательности случайных чисел

Тогда при длине выборки N ожидаемое число появлений случайных чисел x_i с j единицами в проверяемых l разрядах будет равно:

.

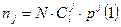Здесь 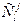– число комбинаций (сочетаний) j единиц в l разрядах; 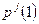– вероятность появления единицы в двоичном разряде; .

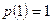Для полученной последовательности определяется эта же характеристика. Проверка соответствия реального значения числа появлений теоретическому выполняется с помощью одного из статистических критериев согласия.

Проверка независимости проводится на основе вычисления корреляционного момента. Напомним, что две случайные величины а и b называются независимыми, если закон распределения одной из них не зависит от того, какое значение приняла другая. Для независимых случайных величин корреляционный момент равен нулю.

Для оценки независимости элементов последовательности поступают следующим образом. Вводят в рассмотрение дополнительную последовательность Y, в которой yi=xi+t, где t – величина сдвига последовательности Y относительно исходной последовательности X. Вычисляют коэффициент корреляции случайных величин X и Y, для чего используются специальные расчетные соотношения.