Алгоритм вычитания двоичных чисел

Из математики известно, что операцию вычитания двух чисел можно заменить операцией сложения, если в качестве вычитаемого взять число, знак которого противоположен исходному, т.е.

R= A – B = A + (- B)

Использование такого подхода позволяет значительно упростить тех­ническую реализацию АЛУ, так как для выполнения операции вычитания можно использовать схемы сумматоров. При этом весьма актуальным является вопрос представления отрицательных чисел в виде двоичных кодов.

На практике для представления отрицательных чисел наибольшее распространение получил метод, в котором для обозначения знака используется старший разряд его двоичного кода. Знаковый разряд при записи обычно отделяют точкой. Так, если используется 8-разрядный двоичный код, то семь его разрядов содержат информацию о величине (модуле) числа, а восьмой (старший) - о его знаке. Таким образом формируется прямой код двоичного числа. Присутствие в знаковом разряде нуля означает, что число положительное, присутствие единицы - что число отрицательное. Следовательно, используя 8-разрядный код, можно записать числа с десятичными эквивалентами от -127 до +127.

Пример 1:

Записать число А = 1100101 в прямом коде.

Решение:

Поскольку число положительное, то в знаковый разряд ставим 0. в результате получим:

Апрк = 0.1100101

Пример 2:

Записать число А = -1100101 в прямом коде.

Решение:

Поскольку число отрицательное, то в знаковый разряд ставим 1. в результате получим:

А прк = 1.1100101

Однако присутствие знакового разряда непосредственно не позволяет использовать рассмотренные ранее схемы сумматоров для выполнения операции вычитания чисел, представленных в прямом двоичном коде.

Наиболее часто для записи отрицательного числа используется дополнительный код.

Алгоритм получения дополнительного кода отрицательного двоичного числа сводится к следующему:

- записывают обратный код исходного числа, для чего все его разряды инвертируют;

- к полученному после инвертирования коду прибавляют единицу.

- в знаковый разряд (крайний слева) ставят единицу, говорящую о том, что число отрицательное.

В дальнейшем, при сложении полученного таким образом кода вычитаемого с кодом уменьшаемого будет реализована операция вычитания. Таким образом, операция вычитания в цифровой технике заменяется операцией сложения с использованием дополнительного кода вычитаемого, т.е.

R= A – B = A + (- B дк)

При этом знак результата определяется старшим разрядом полученного кода. Если старший разряд равен нулю, получено положительное число, представленное в прямом коде. Если старший разряд равен единице, получено отрицательное число, представленное в дополнительном коде. Проиллюстрируем сказанное на примере.

Пример 3. Используя дополнительный код, найти разность R= A – B если А=0011111 (31₁₀), В=0001100 (12₁₀). Решение:

Для решения воспользуемся выражением R= A – B = A + (- B дк)

Поскольку А – положительное, запишем его в прямом коде

А = 0.0011111

Найдем дополнительный код вычитаемого:

- проинвертируем исходное число и прибавим к нему единицу

+

1

Допишем знаковый разряд. В результате получим

Вдк = 1.1110100

Произведем суммирование прямого кода уменьшаемого с дополнительным кодом вычитаемого:

0.0011111

+

1.1110100

10.0010011

Полученный результат представлен 9-разрядным двоичным кодом. В этом случае самый старший разряд отбрасывают, таким образом получен ответ R = 0.0010011. Полученное двоичное число содержит нуль в знаковом разряде. Поэтому результат положителен и представлен в прямом коде. Нетрудно видеть, что его десятичный эквивалент равен 19.

Пример 4. Используя дополнительный код, найти разность R= В – A для тех же исходных данных. Решение:

Для решения воспользуемся выражением R= B – A = B + (-A дк)

Поскольку В – положительное, запишем его в прямом коде

В = 0.0001100

Найдем дополнительный код вычитаемого:

- проинвертируем исходное число и прибавим к нему единицу

+

1

Допишем знаковый разряд. В результате получим

Адк = 1.1100001

Произведем суммирование прямого кода уменьшаемого с дополнительным кодом вычитаемого:

0.0001100

+

1.1100001

1.1101101

Знаковый разряд полученного результата равен единице. Следовательно, получено отрицательное число, записанное в дополнительном коде. Для получения прямого кода можно воспользоваться приведенным выше алгоритмом преобразования прямого кода в дополнительный. Результатом такого преобразования будет прямой код числа:

1.1101101

+

1

1.0010011

Проделав описанные действия с полученным кодом, получим

Апрк = 1.0010011 что с учетом знака эквивалентно числу - 19.

Вывод:: использование при представлении отрицательных чисел дополнительного кода позволяет применить для выполнения операции сложения и вычитания единую логическую схему.

Реализация операции арифметического сложения и вычитания

Рассмотрим часть структурной схемы логического устройства (рис. 11), предназначенного для выполнения операций арифметического сложения и вычитания. Для упрощения приведено только два разряда устройства. Схема состоит из общего управляющего узла на элементе 2ИЛИ (DD1) и блоков сложения-вычитания (БСВ), число которых равно разрядности кодов слагаемых (в данном случае двум). Схема имеет два входа управления:

вход сложения «+» и вход вычитания «–», а также входы для ввода слов данных. С выхода устройства снимаются сигналы суммы и переноса в более старшие разряды. Между сумматорами БСВ реализован принцип последовательного переноса.

В исходном состоянии на входы управления режимом работы устройства поданы сигналы лог. 0. При этом на первые входы элементов 2И DD5, DD9 и элементов 2И сложной логики DD3 и DD6 поданы активные логические сигналы. Вследствие этого на всех входах одноразрядных сумматоров независимо от значения входных кодов слагаемых присутствуют нулевые сигналы. Соответственно равны нулю и выходные сигналы схемы.

Предположим, что на вход сложения «+» подан сигнал лог. 1. В этом случае на первые входы элементов 2И DD5 и DD9, а также первые входы верхних элементов 2И элементов сложной логики DD3 и DD6 будут поданы пассивные логические сигналы (сигналы лог. 1). На первые входы нижних элементов 2И в DD3 и DD6 по-прежнему будут поданы активные логические сигналы. Поэтому на входах сумматоров DD4 и DD8 будут присутствовать сигналы, значения которых определены кодами слагаемых. С выхода устройства будут сняты сигналы, равные результату сложения, и сигнал переноса.

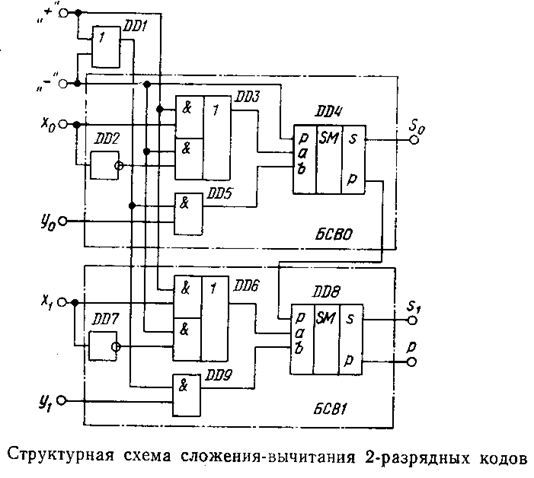
Если сигнал лог. 1 будет подан на вход вычитания, то на первые входы элементов 2И DD5 и DD9 по-прежнему будет подан пассивный логический сигнал и на входы «b» сумматоров поступит прямой код уменьшаемого. На первые входы верхних элементов 2И в DD3 и DD6 придут активные, а на аналогичные входы нижних элементов 2И – пассивные логические сигналы. В результате этого код вычитаемого попадает на входы «а» сумматоров через инверторы, т. е. инвертированным. Одновременно на вход переноса сумматора DD4 нулевого разряда появится единичный сигнал. Учитывая сказанное в предыдущем разделе, можно сказать, что на входы «а» сумматоров будет подан дополнительный код вычитаемого. Поэтому на выходах сумматоров будет сформирован сигнал разности двух кодов У–X.

Очевидно, что подача на оба управляющих входа схемы сигналов лог. 1 является недопустимой, так как это нарушает ее работу.

Таким образом, рассмотренная схема позволяет получить на выходе сигнал либо суммы, либо разности двух двоичных кодов. Вид выполняемой операции определяется значением управляющего сигнала.