Моделювання АД у фазній системі коордінат

Для вирішення завдань, що виходять за рамки лінеарізованной моделі, необхідно моделювати АД по повній системі рівнянь.

При складанні рівнянь використовуються наступні допущення, пов'язані з поняттям ідеалізована машина:

- сталь машини ненасичена;

- фазні обмотки симетричні і зрушені в просторі на ;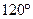

- МРС обмоток і магнітні поля розподілені синусоїдальний уздовж кола повітряного зазору;

- ротор електрично і магнітно симетричний;

- реальні розподілені обмотки АД замінюються зосередженими, а її МРС прийнята МРС реальної обмотки.

Для опису перехідних процесів в АД необхідно скласти рівняння електричної рівноваги для всіх контурів, і рівняння руху ротора.

АД представляють як систему магнітосвязанних обмоток, розташованих на статорі і роторі.

Рівняння електричної рівноваги контурів для статора і ротора::

; ;

; ;

; .

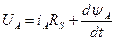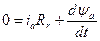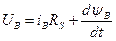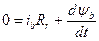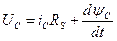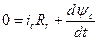де 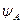, , 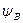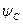- потокощеплення фаз статора; 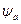, , 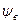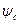- потокощеплення фаз ротора; 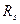, 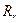- активні опори фаз статора и ротора.

Потокощеплення будь-якої фази АД визначається величиною власної індуктивності і взаємної індуктивності із всіма іншими обмотками.

Наприклад, для фази А

;

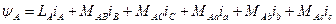де 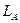- індуктивність фази; 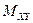- взаимоиндуктивность між обмотками X і Y.

Виходячи з прийнятих допущень про симетричність електричної машини:

- взаємні індуктивності між обмотками статора

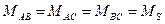
- взаємні індуктивності між обмотками ротора

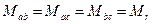
Наиболее сложными моментами при моделировании является то, что взаимное пространственное расположение обмоток ротора и статора изменяется, вследствие чего изменяется и величина взаимной индуктивности между этими обмотками.

Найбільш складними моментами при моделюванні є те, що взаємне просторове розташування обмоток ротора і статора змінюється, унаслідок чого змінюється і величина взаємної індуктивності між цими обмотками.

Максимальне значення взаїмоїндуктівності відповідає збігу осей двох фаз, при перпендикулярному розташуванні осей буде М рівна нулю. Тому взаємна індуктивність між обмотками статора і ротора змінюватиметься по гармонійному закону.

Для фази А

,

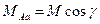де М – максимальна величина взаємної індуктивності; 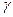- кут повороту ротора.

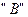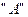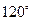Фаза випереджає на , тоді

;

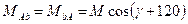Аналогічно для фази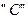

;

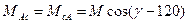Аналогічно для фаз 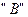і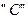

;

;

.

;

;

.

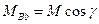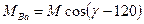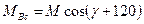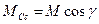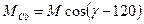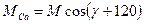Тепер рівняння потокосцепленія фази в розгорненому вигляді:

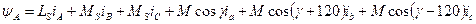
Враховуючи 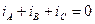, то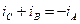

.

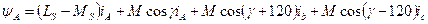Тепер рівняння електричної рівноваги: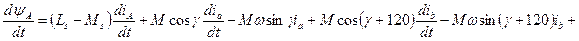

,

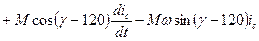Звідки

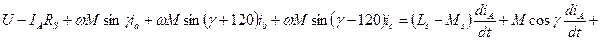
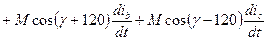
При цьому в системі рівнянь АД відсутні потокосцепленія, а як невідомі функції використовуються струми. Тому ця система – система щодо струмів. Недоліки:

- система ДР нелінійна, оскільки містить обчислень функцій від шуканих функцій (sin і cos кута повороту );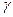

- система ДР непредставіма в канонічній формі, вирішеній відносно похідних, оскільки в правій частині кожного рівняння міститься 4 похідних від невідомих функцій.

Рішення такий систему можливо при використанні наступного алгоритму:

1. використовуючи інформацію про початкові значення струмів, швидкості і кута повороту знаходять поточні значення струмів, швидкості і кута повороту находят поточні значення взаємних індуктівностей між обмотками статора і ротора;

2. обчислюють праві частини рівнянь електричної рівноваги всіх фаз;

3. систему з 5 рівнянь розглядають як систему лінійних рівнянь алгебри щодо похідних струмів. Застосовуючи чисельні методи рішення систем лінійних рівнянь (Крамера, Гауса, обертання і ін.) знаходять похідні струмів; 4. чисельно інтегрують систему ДР і знаходять невідомі.

Дуже складно вирішувати систему ДР і відносно потокосцепленій, оскільки струми складним чином залежать від потокосцепленій всіх обмоток. Тут можна, задаючись початковими значеннями потокосцепленій, з системи рівнянь для потокосцепленій, вирішуючи її як систему лінійних рівнянь, визначити струми.

Таким чином систему ДР АД у фазній системі координат можна використовувати для розрахунку перехідних процесів. Основний недолік – громіздкість; велика кількість нелінійних елементів; необхідність вирішувати проміжну систему лінійних рівнянь.