Б) Вимушені коливання в системі при наявності демпфірування
Розглянемо випадок, коли сила опору середовища, що діє на і-ту точку системи, пропорційна першому степені швидкості 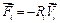 , де
, де 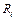 - коефіцієнт сил тертя, що визначається звичайно експериментально.
- коефіцієнт сил тертя, що визначається звичайно експериментально.
Знайдемо узагальнену силу опору середовища, скориставшись загальним виразом для узагальненої сили і тим, що 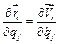
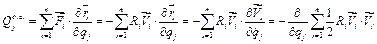 .
.
Введемо поняття функції розсіювання, або дисипативну функцію Релея
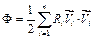 .
.
Для системи зі стаціонарними в'язями
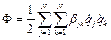 ,
,
де 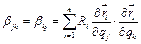 , крім того
, крім того 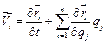 ,
,
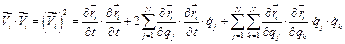 .
.
Якщо система має один ступінь вільності, то
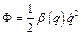 .
.
Отже, функція розсіювання є однорідною квадратичною функцією узагальнених швидкостей з коефіцієнтами, що залежать від узагальнених координат. Таким чином,
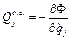 .
.
Для системи з одним ступенем вільності
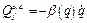 , або
, або 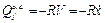 .
.
Враховуючи вищевикладене, диференціальне рівняння руху системи з одним ступенем вільності, з урахуванням сил опору середовища, що змінюється за лінійним законом, має вид
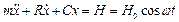 (4.8)
(4.8)
Для більшості акустичних процесів, пов'язаних з випромінюванням звуку характерними є сферичні хвилі, які найкраще описуються степеневими функціями. Тому, диференціальне рівняння (4.8), що описує вимушені коливання в системі при наявності демпфірування, може бути представлено також у виді
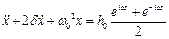 ,
,
де 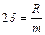 ;
; 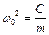 ;
; 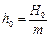 ;
; 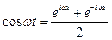 . (4.9)
. (4.9)
Побудуємо його розв'язок методом комплексних амплітуд.
1) Розглянемо спочатку диференціальне рівняння:
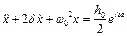 (4.10)
(4.10)
Розв'язок цього рівняння складається з суми двох функцій
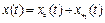 .
.
Перший доданок може бути знайдений з розв'язку однорідного рівняння
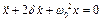 .
.
Тоді
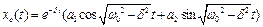 , (4.10)
, (4.10)
де а1 і а2 – сталі, що знаходяться з початкових умов.
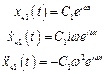
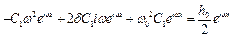
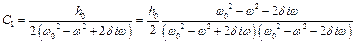
Зробимо заміну 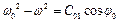 та
та 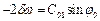 ,
,
тобто 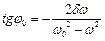 . Звідси
. Звідси
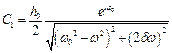 .
. 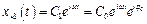 ,
,
де 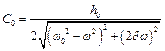
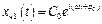 .
.
2) Розглянемо тепер рівняння
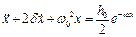 ; (4.11)
; (4.11)
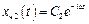 ;
;
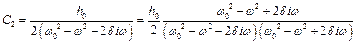 .
.
Замінимо 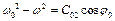 та
та 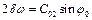 , звідки
, звідки
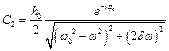 ,
, 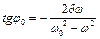
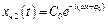
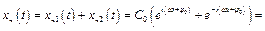
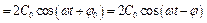 , бо
, бо 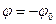
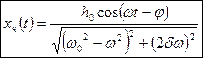
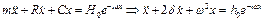 (4.12)
(4.12)
В зв'язку з тим, що коефіцієнти рівняння дійсні числа, шукаючи його частинний розв'язок від збурюючої сили у вигляді комплексної функції необхідно спочатку знайти комплексний розв'язок рівняння, а потім для відшукування залежності, що описує рух реальної фізичної системи, виділити тільки його дійсну частину. Фактичне виконання такої операції у задачах акустики часто непотрібно, бо усі необхідні відомості вдається добути безпосередньо з комплексного розв'язку.
Знайдемо частинний розв'язок рівняння символічним методом
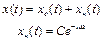
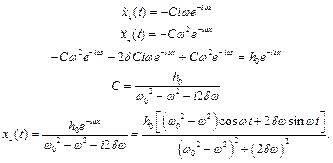
Введемо позначення:
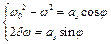 ;
; 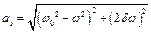 ;
; 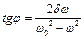
Звідси 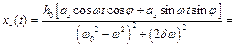
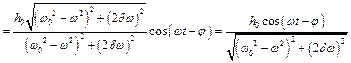
Частинний розв'язок рівняння (4.12) отриманий символічним методом повністю співпадає з розв'язком рівняння (4.9) методом комплексних амплітуд. Таким чином, загальний розв'язок диференціального рівняння (4.8), що описує вимушені коливання в системі з урахуванням сил опору середовища має вид

|
| рис. 4.9 |
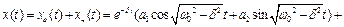
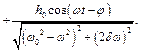 (4.13)
(4.13)
В режимі усталених коливань (при t→∞) останній вираз має вид:
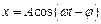 ,
,
де 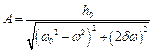
Знайдемо закон зміни швидкості
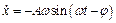 ;
;
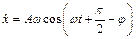
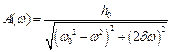 -амплітуда вимушених коливань.
-амплітуда вимушених коливань.
Введемо позначення:
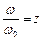 - безрозмірна частота;
- безрозмірна частота;
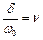 - безрозмірний коефіцієнт демпфірування;
- безрозмірний коефіцієнт демпфірування;
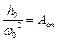 - статичне зміщення в системі.
- статичне зміщення в системі.
Тоді 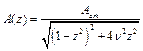 або
або 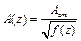 .
.
Якщо в деякій точці функція f(z) приймає мінімальне значення, то А(z) має максимум в цій точці. Знайдемо екстремуми f(z).
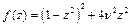 ;
; 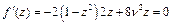 ;
; 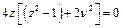

|
| рис. 4.10 |
1) 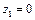 ;
;
2) 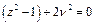 ;
; 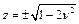 .
.
Беремо тільки позитивні значення для z, отже 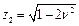 .
.
Звідси 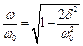 , тобто
, тобто 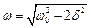 .
.
Знайдемо другу похідну f(z):
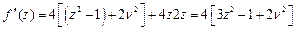 ;
;
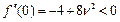 , тобто в точці z=0 функція f(z) має максимум, а А(z) – мінімум.
, тобто в точці z=0 функція f(z) має максимум, а А(z) – мінімум.
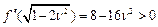 - в
- в 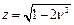 функція f(z) має мінімум, а А(z) – максимум.
функція f(z) має мінімум, а А(z) – максимум.
Залежність амплітуди вимушених коливань від частоти А(ω) наведена на рис.4.10 (крива 1).
Якщо частота зовнішньої сили збігається з власною частотою системи, то виникає така ситуація, коли система здатна споживати усю енергію, закладену в джерелі. При цьому говорять про виникнення явища резонансу. Частота, на якій виникає резонанс називається резонансною.
Дослідимо залежність амплітуди швидкості від частоти.
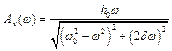 , або
, або
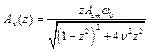 . Тоді
. Тоді 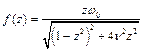
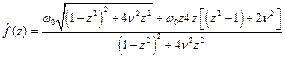
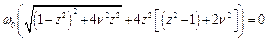
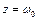
Дата добавления: 2020-08-31; просмотров: 935;











