Метод векторів, що зображають
Розглянемо трифазну систему координатних осей, нерухому в просторі.
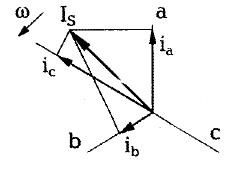
З центру системи координат проведемо вектор, причому довжину вектора виберемо рівній амплітуді фазного струму.
При обертанні вектора 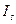 з кутовою швидкістю
з кутовою швидкістю 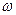 проекції цього вектора на координатні осі будуть рівні:
проекції цього вектора на координатні осі будуть рівні:
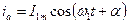 ;
;
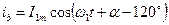 ;
;
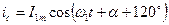 ,
,
де 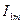 - амплітуда фазного струму,
- амплітуда фазного струму, 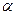 - фазовий кут.
- фазовий кут.
Таким чином за допомогою одного вектора, що обертається, можна утворити симетричні синусоїдальні струми фаз.
Цей вектор називають зображаючим. Його можна представити у вигляді 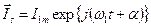
Зображаючий вектор 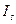 зв’язаний зі значеннями фазних струмів виразами:
зв’язаний зі значеннями фазних струмів виразами:
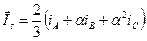 ,
,
де 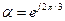
Аналогічно можна представити зображаючі вектори, для напруги, потокощеплень статора і ротора.
Запишемо рівняння електричної рівноваги для статора:
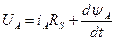 ;
;
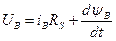 ;
;
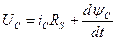 .
.
І помножимо рівняння фази 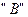 на
на 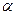 , а фази
, а фази 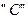 на
на 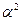 , складаємо і отримуємо одне рівняння для вектора напруги, що зображає:
, складаємо і отримуємо одне рівняння для вектора напруги, що зображає:
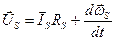 .
.
Для ротора
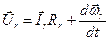 .
.
Электромагнітний момент АД
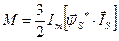 ,
,
де 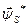 - сопряженний комплекс потокосцепленія статора;
- сопряженний комплекс потокосцепленія статора; 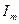 - операція узяття уявної частини.
- операція узяття уявної частини.
Вектори струмів і потокосцепленій зв'язані між собою лінійними співвідношеннями:
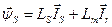
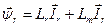
Таким чином, модель АД у векторах, що зображають, має вигляд:
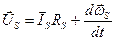 ;
;
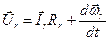 ;
;
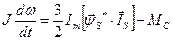 .
.
Але цією системою рівнянь можна користуватися тільки для аналізу симетричних режимів.
Дата добавления: 2021-01-11; просмотров: 472;











