Рівняння АД в ортогональній системі координат

З розглянутих моделей АД видно, що рівняння в трифазній системі координат є громіздкими і такими, що погано піддаються рішенню. Для спрощення системи ДР АД доцільно використовувати метод лінійної заміни змінних.

Лінійне перетворення змінних полягає в тому, що початкові змінні в рівняннях замінюють на нові, лінійно пов'язані з результатними. Так замість струмів статорів 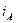, , 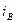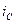вводять нові струми , ,

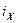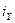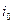
Визначувані наступними залежностями::

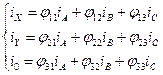
Лінійне перетворенні повинно бути однозначним, для чого у будь-який момент часу повинна виконуватися нерівність:

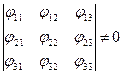або .

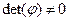Виберемо струм 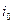у вигляді 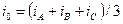. Зручність такого вибора полягає в тому, що часто (для зірки з ізольованою нейтральною крапкою).

Розглянемо, як виражаються струми 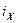і 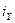через фазні струми. Виразимо 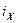і 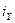як проекції зображуючого вектора. Для зображення двох струмів необхідно вибрати дві осі і прийняти ці осі ортогональними.

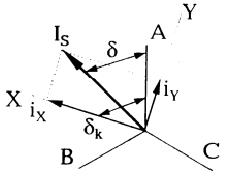
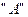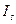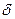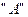Кут між і складає , між і Х - 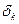. У загальному випадку координатна система XY обертається в просторі з постійною швидкістю .

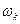Проекції вектора, що зображає, на осі А, В, С

;

;

.

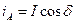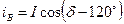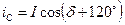У ортогональній системі XY:

;

.

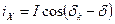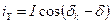Використовуючи тригонометричну тотожність остаточно отримаємо:

;

.

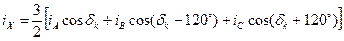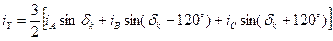Оскільки, в об щем випадку, система координат XY обертається в просторі со швидкістю 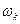, то 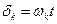, і струми еквівалентних контурів статора і ротора пов'язані з фазними наступними співвідношеннями:

;

;

;

.

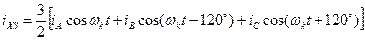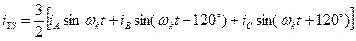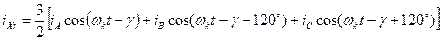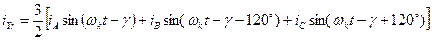Формули зворотних перетворень

- для статора

;

;

.

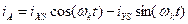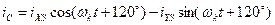- для ротора

;

;

.

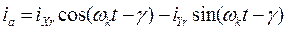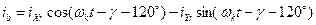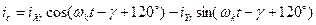Якщо реальна фазна напруга визначаються співвідношенням

;

;

,

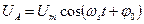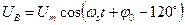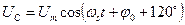то напруга в перетвореній системі:

;

.

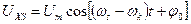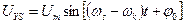Тепер рівняння АД матимуть вигляд:

;

;

;

;

.

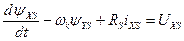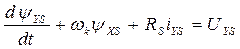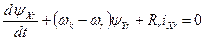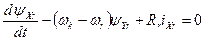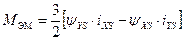Потокощеплення еквівалентних контурів:

;

;

;

.

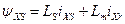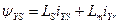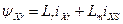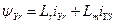У теорії моделювання електромагнітних і електромеханічних процесів в електричних машинах розглядають 3 основні координатні системи, яка є окремими випадками розглянутої ортогональної системи..

1. Координатна система, нерухома щодо ротора - .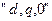

Ця система знаходить найбільше застосування при аналізі синхронних і асинхронних машин при несиметрії ротора. Зручність цієї системи в тому, що електрична машина, в магнітному відношенні, виявляється симетричною незалежно від кутового положення ротора.

Система 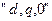є єдиною, ДР синхронної машини, що приводить, до системи рівнянь з постійними коефіцієнтами.

Оскільки 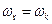, то перетворена напруга

;

.

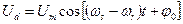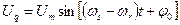Є несинусоїдальними функціями часу.

2. Координатна система, нерухома щодо статора АД - 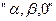, в ній 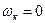. Ця система координат знаходить застосування при моделірованіі АД в симетричних режимах роботи. Вісь 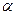співпадає з віссю .

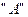Перетворена напруга

;

.

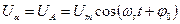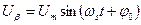При такому напрямі 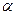всі перетворені змінні на цій осі співпадають з реальними фазними змінними.

3. Координатна система, нерухома щодо поля статора - 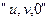, в ній 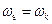. Система знаходить застосування при дослідженні частотно керованих електроприводів і груп електричних машин що працюють від загальної мережі.

Перетворена напруга

;

,

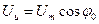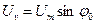І є постійними величинами.