Вимушені коливання в системі з двома ступенями вільності при наявності сил опору.

рис. 4.18

Запишемо рівняння Лагранжа другого роду для двохмасової системи з урахуванням сил опору середовища та кінематичного і силового збурення одночасно (рис.4.18):

1) ;

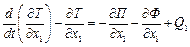2) .

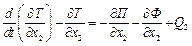Запишемо кінетичну, потенціальну енергії системи та дисипативну функцію Релея для цього випадку:

;

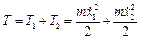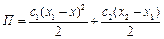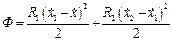; ; Q₁=0 , Q₂=H.

Знайдемо необхідні похідні:

; ; ; ;

; ;

; .

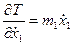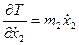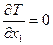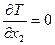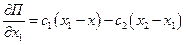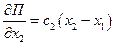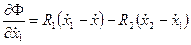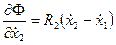Отже, отримаємо систему рівнянь:

;

;

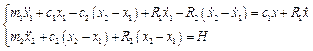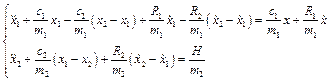
Введемо позначення ; ; ; ; ; .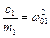

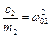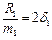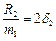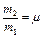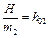Тоді,

.

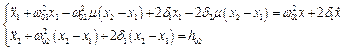Ввівши оператор диференціювання 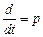отримаємо

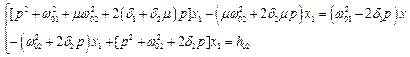
Представимо збурюючу силу в формі

;

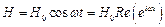або в символічній формі 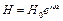, а

.

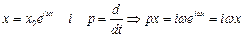Тоді, для гармонічного процесу

; .

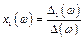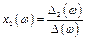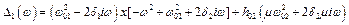
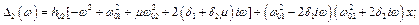
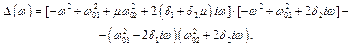
Розглянемо деякі часткові випадки.

1. Нехай маємо двохмасову систему лише з кінематичним збуренням без демпфера між масами , , .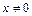

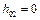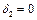Тоді маємо

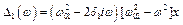
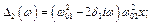
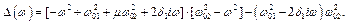
Якщо налаштувати систему так, щ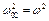о , то

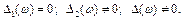
Це означає, що при такому співвідношенні параметрів тіло масою m₁ нерухоме, а тіло масою m₂ здійснює коливання. Цей ефект називається динамічним гасінням коливань і пояснюється так.

На тіло, масою m₁ з одного боку через пружину с₁ передається кінематичне збурення, а з другого – через пружину с₂ діє тіло масою m₂. Якщо ці сили однакові за величиною і протилежно напрямлені, то головний вектор сил, прикладених до тіла масою m₁, дорівнює нулю.

рис. 4.19

2. Нехай маємо лише силове збурення, сили опору в двохмасовій системі відсутні , , .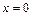

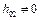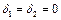Тоді

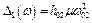
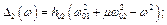
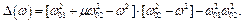
Якщо налаштувати систему так, щ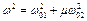о , то 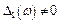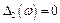, 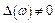. Тобто, тіла 1 і 2 наче міняються ролями. Характер зміни амплітуди коливань А₁ тіла масою 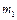залежно від частоти збурення зображено на рис.4.19. На рисунку показані парціальні частоти ω₀₁ і ω₀₂, і частоти нормальних коливань ω₁ і ω₂, що розміщені на осі Оω згідно теореми Релея. Залежність A₁(ω) зображених на рис.4.19 суцільною лінією при δ₂=0 і штрих-пунктирною при δ₂≠0. Аналіз результатів показує, що для зменшення амплітуди коливань в двохмасовій системі досить ввести демпфер лише в одному місці.