Интервал и радиус сходимости степенного ряда

Из теоремы Абеля следует, что если 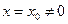есть точка сходимости степенного ряда, то интервал (-| 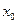|;| |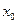) весь состоит из точек сходимости данного ряда при всех значениях х, а вне этого интервала ряд расходится. Положив | 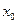|=R, интервал можно записать в виде (-R;R). Этот интервал называется интервалом сходимости. Число R называют радиусом сходимости, т.е. R>0 – это такое число, что при всех х, для которых |x|<R ряд абсолютно сходится, а при |x|>R ряд расходится.

В частности, когда ряд сходится лишь в одной точке 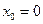, то R=0, если же ряд сходится при всех значениях 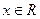, то R=∞. Сходимость ряда на концах интервала сходимости при 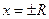проверяют отдельно.

Радиус сходимости можно найти по формуле, которая следует из признака Даламбера:

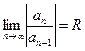(14.8)

Используя радикальный признак Коши, можно установить, что

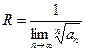(14.9)

Замечания:

1) Если 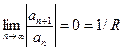, то ряд абсолютно сходится на всей числовой оси. В этом случае R=∞. Если 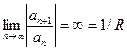, то R=0.

2) Интервал сходимости степенного ряда (14.7) находят из неравенства .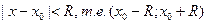

3) Если степенной ряд содержит не все степени х, т.е. задан неполный степенной ряд, то интервал сходимости находят без определения радиуса сходимости, а непосредственно применяют признак Даламбера (или Коши) для ряда, составленного из модулей исходного ряда.

Пример 2.2. Найти область сходимости ряда: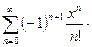

Решение: 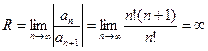, т.е. ряд абсолютно сходится на всей числовой оси.

Пример 2.2. Найти область сходимости ряда и исследовать его сходимость на концах интервала сходимости:

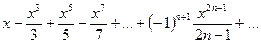
Решение:Ряд неполный, поэтому используем признак Даламбера:

;

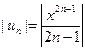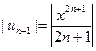
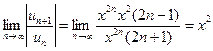По признаку Даламбера ряд абсолютно сходится при l<1, т.е. .

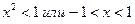Исследуем сходимость ряда на концах полученного интервала сходимости.

При х=-1 имеем ряд -1+1/3-1/5+1/7-1/9+… Этот ряд сходится по признаку Лейбница.

При х=1 имеем ряд 1-1/3+1/5-1/7+… Этот ряд также сходится по признаку Лейбница.

Следовательно, область сходимости ряда [-1;1].

Лекция 15