Теорема 2. Предельный признак сравнения.

Пусть даны два знакоположительных ряда (1) и (2). Если существует конечный, не равный нулю, предел 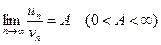, то ряды (1) и (2)сходятся или расходятся одновременно.

Пример 2. Исследовать сходимость ряда:

Решение. Сравним данный ряд с рядом геометрической прогрессии . Этот ряд сходится, т.к. q=1/2<1. Мы имеем . Следовательно, по теореме 1 исходный ряд сходится.

Пример 3. Исследовать сходимость ряда: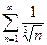

Решение. Сравним данный ряд с гармоническим расходящимся рядом.

Мы имеем . Следовательно, исходный ряд расходится.

Ряд, с которым сравнивают исследуемый ряд, называется эталонным.

В качестве эталонных рядов используются:

1) гармонический ряд 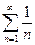Он расходится.

2) обобщенный гармонический ряд . При α>1 ряд сходится, а при 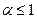- расходится.

3) Геометрический ряд 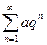. Ряд сходится при |q|<1, и расходится при .

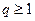Замечания:

a) при решении примеров иногда требуется отбросить несколько членов ряда, если сначала есть отрицательные члены, а затем ряд знакоположительный. По третьему свойству это не влияет на сходимость ряда.

b) Если общий член ряда представляет собой отношение двух многочленов, то при подборе эталонного обобщенного гармонического ряда значение α выбирают равным разности наибольших показателей степеней знаменателя и числителя.