Ряд геометрической прогрессии

Это ряд:

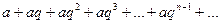(13.6)

где 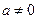- некоторое число, q – знаменатель геометрической прогрессии.

Как известно, сумма первых n членов геометрической прогрессии находится по формуле:

(13.7)

Найдем предел этой суммы: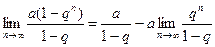

Рассмотрим следующие случаи в зависимости от величины q:

1) |q|<1, то 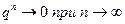, поэтому ,

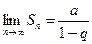т.е. ряд сходится и его сумма равна 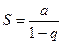(13.8).

2) |q|>1, то 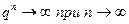, поэтому 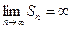и ряд расходится.

3) |q|=1, то при q=1 ряд принимает вид 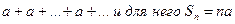и

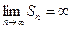, ряд расходится. При q=-1 ряд принимает вид 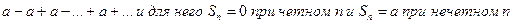. Следовательно, 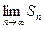не существует и ряд расходится.

Вывод: ряд геометрической прогрессии сходится при |q|<1, и расходится при .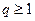

Необходимый признак сходимости числового ряда

Гармонический ряд

Теорема. Необходимый признак сходимости числового ряда.

Если ряд (13.1) сходится, то его общий член стремится к нулю, т.е. .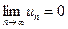

Следствие. Достаточное условие расходимости ряда.

Если 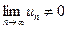или предел не существует, то ряд расходится.

Пример 1. Исследовать сходимость ряда: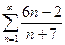

Решение:

.

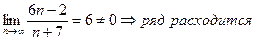Гармоническим рядом называется ряд:

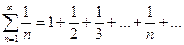
Данный ряд расходится (доказательство не приводим), хотя 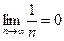, так как этот признак не является достаточным для того, чтобы утверждать, что ряд сходится.