Member; // очередной член ряда
printf ("Input value of argument:");
scanf("%lf",&x);
printf ("\nInput precision:");
scanf("%lf",&eps);
for (i=2, member=x; fabs(member)>eps; i++) // проверка точности
{
res = res + member; // добавление в сумму нового члена ряда
member = member*x/i; // вычисление следующего члена ряда
}
printf ("\ny= %.40lf\nprecision: %.40lf\n",res,member);
printf ("number of series members: %u\n",i);
getch();
}
5. Методы нахождения корней уравнения: половинного деления, хорд, касательных, простой итерации.
Пусть задано уравнение вида f(x)=0, и известно, что на отрезке [a,b] оно имеет один корень, т.е. в точках a и b значения функции имеют разные знаки.
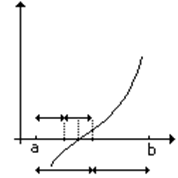
Если |a-b|<ε, где ε – требуемая точность вычислений, то любое значение x из заданного интервала (например, a) можно считать искомым корнем. Иначе в качестве приближения корня возьмем середину отрезка xi=(a+b)/2. Если значение функции f(xi)=0, то решение найдено. Иначе выбираем тот из отрезков ([a,xi],[xi,b]), на концах которого значения функций имеют разные знаки, и следующий шаг алгоритма реализуем относительно этого отрезка.
Указанный алгоритм известен в литературе как метод половинного деления.
Заменим теперь исходное уравнение f(x)=0 на равносильное ему уравнение вида x=φ(x). Пусть на отрезке [a,b]оно содержит только один корень. Выберем в качестве первого приближения некоторое xi 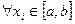 . Последующие приближения получаем по формуле xi+1=φ(xi). Если данная последовательность сходится, то она сходится к корню уравнения.
. Последующие приближения получаем по формуле xi+1=φ(xi). Если данная последовательность сходится, то она сходится к корню уравнения.
Описанный алгоритм носит название метода простой итерации.
Пусть функция имеет на отрезке один корень. Точки A и B имеют координаты A(a,f(a)) и B(b,f(b). Искомым корнем будет абсцисса c точки пересечения графика с Ox. Вместо нее ищется точка пересечения хорды AB с Ox.
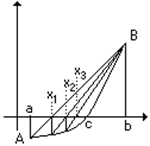
Уравнение прямой, проходящей через точки A и B, записывается в виде:
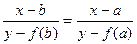
Первое приближение x1 получаем подстановкой y=0:
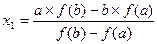 или
или 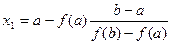 или
или 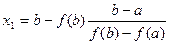
Последующие приближения будем вычислять по формулам
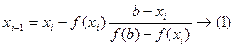
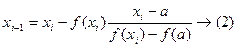
При этом, если f(xi)*f(b)<0 (т.е. f(xi) и f(b) разных знаков) то последующие приближения вычисляются по формуле (1), иначе – по формуле (2).
Если на отрезке [a,b] существует первая и вторая производные указанной функции, сохраняющие постоянный знак, то последовательность xi монотонно сходится к корню уравнения f(x)=0.
Рассмотренный алгоритм представляет известный метод хорд.
Немного иначе устроен метод касательных. В этом случае приближение осуществляется на основе замены дуги касательной, проведенной к одной из крайних точек.
Итерационная формула описывается как:
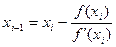
Если на отрезке [a,b] f’(x)*f’’(x)>0 , то нулевое приближение корня – это значение x0=b, иначе x0=a.
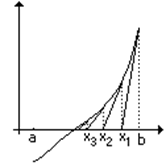
Пусть у нас задана функция y=x2-3. При x=1 – y=-2, а при x=2 – y=1. Это как раз наш случай – на интервале [1,2] – есть корень. Программа, реализующая поиск корня по методу касательных, может выглядеть так:
#include <stdio.h>
#include <math.h>
#include <conio.h>
//////////////////////// Вычисление функции
double func(double x) { return (x*x - 3.0); }
//////////////////////// Вычисление производной функции
double derfunc(double x) { return (2*x); }
////////////////////////////////// Реализация метода касательных
int newton(double (*f)(double), // Функция
double (*f1)(double), // Производная функция
Дата добавления: 2022-02-05; просмотров: 559;











