Ряды Тейлора и Маклорена

Для любой функции f(x), определенной в окрестности точки 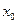и имеющей в ней производные до (n+1)-го порядка включительно, справедлива формула Тейлора:

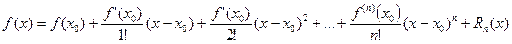(15.1)

где 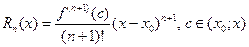(15.2) – остаточный член в форме Лагранжа. Число с можно записать в виде .

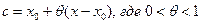Формулу (15.1) можно записать в виде:

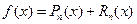(15.3),

где 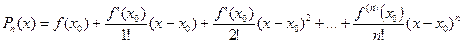(15.4) – многочлен Тейлора.

Если функция имеет производные любых порядков (т.е. бесконечно дифференцируема) в окрестности точки 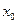и остаточный член 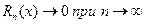( 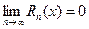), то из формулы Тейлора получается разложение функции f(x) по степеням 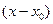, которое называется рядом Тейлора:

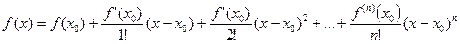(15.5)

Если в ряде Тейлора положить 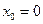, то получим разложение функции f(x) по степеням х в ряд Маклорена:

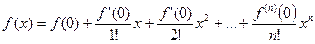(15.6)

Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки 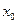. Но отсюда еще не следует, что он будет сходиться к данной функции f(x): он может оказаться расходящимся или сходиться, но не к функции f(x). Так например, функция 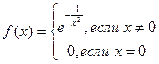имеет в точке х=0 производные всех порядков 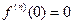при всяком n. Ряд Маклорена имеет вид:

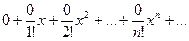Ряд сходится, но его сумма равна 0, а не f(x).

Теорема. Для того, чтобы ряд Тейлора (3.5) сходился к f(x) в точке 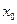, необходимо и достаточно, чтобы в этой точке остаточный член формулы (15.1) стремился к нулю при n→∞, т.е. .

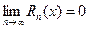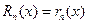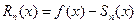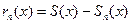Замечание: Если ряд Тейлора (15.5) сходится к порождающей его функции f(x), то остаточный член формулы Тейлора (15.1) равен остатку ряда Тейлора, т.е. (напомним, что , а , где S(x) – сумма ряда Тейлора).