От неограниченных функций (II рода)
Пусть функция 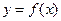 непрерывна на промежутке
непрерывна на промежутке 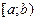 и имеет разрыв II рода при x=b. Тогда несобственные интегралы от неограниченной функции определяются следующим образом:
и имеет разрыв II рода при x=b. Тогда несобственные интегралы от неограниченной функции определяются следующим образом:
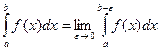 (3.4)
(3.4)
Если предел, стоящий в правой части равенства (3.4) существует, то несобственный интеграл II рода называется сходящимся, в противном случае – расходящимся.
Аналогично, если функция 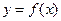 имеет разрыв II рода в точке x=a, то полагают:
имеет разрыв II рода в точке x=a, то полагают:
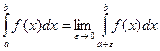 (3.5)
(3.5)
Если функция 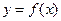 имеет разрыв II рода во внутренней точке
имеет разрыв II рода во внутренней точке 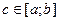 , то
, то 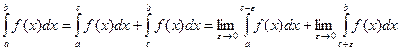 (3.6)
(3.6)
В этом случае интеграл называется сходящимся, если оба правые интегралы сходятся.
Существуют два признака сходимости и расходимости несобственных интегралов II рода:
1. Если на промежутке 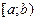 функции
функции 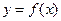 и
и 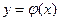 непрерывны, при x=b имеют разрыв II рода и удовлетворяют условиям
непрерывны, при x=b имеют разрыв II рода и удовлетворяют условиям 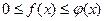 , то из сходимости интеграла
, то из сходимости интеграла 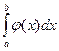 следует сходимость интеграла
следует сходимость интеграла 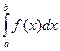 , а из расходимости интеграла
, а из расходимости интеграла 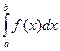 следует расходимость интеграла
следует расходимость интеграла 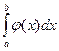 .
.
2. Пусть на промежутке 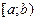 функции
функции 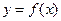 и
и 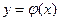 непрерывны и при x=b имеют разрыв II рода. Если существует конечный предел
непрерывны и при x=b имеют разрыв II рода. Если существует конечный предел  , то интегралы
, то интегралы 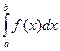 и
и 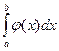 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Примеры.
1) 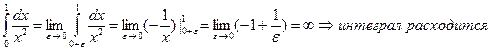
2) 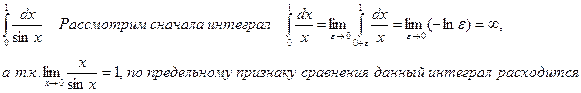
 Лекция 13
Лекция 13
Числовые ряды
Числовым рядом (или просто рядом) называется выражение вида:
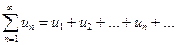 (13.1)
(13.1)
где 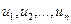 - действительные или комплексные числа, называемые членами ряда;
- действительные или комплексные числа, называемые членами ряда; 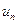 - общий член ряда.
- общий член ряда.
Ряд считается заданным, если известен общий член ряда 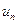 , выраженный как функция его номера n:
, выраженный как функция его номера n:
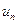 =f(n) (1.2)
=f(n) (1.2)
Сумма первых n членов ряда (13.1) называется частичной суммой ряда и обозначается : 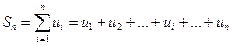 (13.2)
(13.2)
Рассмотрим последовательность частичных сумм:
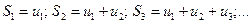
Если существует конечный предел 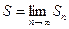 последовательности частичных сумм ряда (13.1), то этот предел называют суммой ряда (13.1) и говорят, что ряд сходится. Записывают сумму ряда так:
последовательности частичных сумм ряда (13.1), то этот предел называют суммой ряда (13.1) и говорят, что ряд сходится. Записывают сумму ряда так:
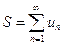 (13.3)
(13.3)
Если 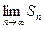 не существует или
не существует или 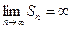 , то ряд называют расходящимся. Такой ряд суммы не имеет.
, то ряд называют расходящимся. Такой ряд суммы не имеет.
Рассмотрим некоторые важные свойства рядов:
1) Если ряд (1.1) сходится и его сумма S, то ряд
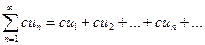 (13.4),
(13.4),
где с – произвольное число, также сходится и его сумма равна сS. Если же ряд (1.1) расходится и с≠0, то и ряд (13.4) расходится.
2) Если сходится ряд (13.1) и сходится ряд 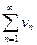 и их суммы равны S1 и S2 соответственно, то сходятся и ряды
и их суммы равны S1 и S2 соответственно, то сходятся и ряды 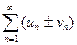 , причем сумма каждого ряда соответственно равна
, причем сумма каждого ряда соответственно равна 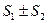 .
.
Следствия:
а) сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд;
б) сумма (разность) двух расходящихся рядов может быть сходящимся или расходящимся рядом.
3) Если к ряду (13.1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (13.1) сходятся или расходятся одновременно.
Следствие: если ряд (13.1) сходится, то его остаток:
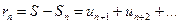 (13.5) стремиться к нулю при n→∞, т.е.
(13.5) стремиться к нулю при n→∞, т.е. 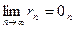 .
.
Дата добавления: 2021-01-11; просмотров: 513;











